Schroedinger Gleichung
Die Schroedinger Gleichung
Schroedinger fasst nach den Erkenntnissen von De Broglie ein Atom als schwingendes System auf. Da jedes sich bewegende Teilchen durch eine Wellengleichung beschrieben werden kann, kann durch loesen der Schroedinger Gleichung eine Wellenfunktion fuer bestimmte Probleme ermittelt werden.
Die Schroedinger Gleichung kann kurz zusammengefasst werden:
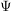 ist eine Funktion, in der Schule nennt man eine Funktion die von x abhaengt auch ist eine Funktion, in der Schule nennt man eine Funktion die von x abhaengt auch 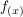 , das koennte man hier auch schreiben, aber die andere Schreibweise hat sich eingebuergert. , das koennte man hier auch schreiben, aber die andere Schreibweise hat sich eingebuergert.
Bei H handelt es sich um den so genannten Hamilton Operator. Operatoren sind in der mathematik Rechenanweisungen. Der Hamilton Operator sieht so aus:
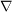 ist wiederum ein Operator der sagt, "leite zwei mal nach dem Ort ab". V ist eine Variable fuer die potentielle Energie. ist wiederum ein Operator der sagt, "leite zwei mal nach dem Ort ab". V ist eine Variable fuer die potentielle Energie.
Der Hamilton Operator sagt also einfach: Du hast eine Funktion, diese leitest Du zwei mal nach dem Ort ab und multipliziere mit dem Bruch. Dazu addierst Du einen Therm fuer die potentielle Energie der Funktion. Klingt etwas umstaendlich, wird aber im Verlauf des Artikels noch klarer, versprochen. :-)
E aus der Schroedinger Gleichung ist ein Energieoperator.
Der Operator sagt also einfach, "Leite Deine Funktion nach t ab und multipliziere mit 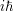 ". i ist dabei die Wurzel aus -1. Und ". i ist dabei die Wurzel aus -1. Und 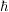 ist gleich ist gleich 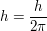 . .
Nun wie man auf so eine Gleichung kommt? Fragt mal den Physiker eures Vertrauens, wir werden nur damit rechnen, die Gleichung aber nicht grundlegend hinterfragen.
Letztendlich kann man die Schroedingergleichung dementsprechend auch so schreiben:
Und was kann man nun damit anstellen? Man kann naeherungsweise berechnen, was fuer eine Farbe ein Molekuel mit konjugiertem  -Elektronensystem aufweist. Ausserdem lassen sich Orbitale formulieren und noch vieles mehr... -Elektronensystem aufweist. Ausserdem lassen sich Orbitale formulieren und noch vieles mehr...
Das Teilchen im Kasten
Nun wollen wir mal etwas konkreter werden. Man stelle sich folgendes vor:
Wir betrachten den eindimensionalen Fall eines Teilchens im Potentialkasten. Ein Ball (ein Elektron) befindet sich zwischen zei unendlich hohen Waenden. Diese Waende haben einen Abstand von L. Damit der Ball ueber die Waende hinaus springen koennte braeuchte er eine unendliche Energie. Da er diese nicht hat muss sich der Ball auf jedenfall zwischen den Waenden befinden. Seine Wahrscheinlich keit zwischen den Waenden (im Potentialtopf) zu sein liegt also bei 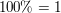 . Ausserhalb des Kastens ist er dementsprechend gar nicht, dort ist seine Aufenthaltswahrscheinlichkeit 0. Logisch oder? Nun sagen wir, dass der Ball nicht wie wild im Kasten herum springt, sondern eine potentielle Energie von 0 hat. . Ausserhalb des Kastens ist er dementsprechend gar nicht, dort ist seine Aufenthaltswahrscheinlichkeit 0. Logisch oder? Nun sagen wir, dass der Ball nicht wie wild im Kasten herum springt, sondern eine potentielle Energie von 0 hat.
Nun sehen wir uns die Schroedinger Gleichung dazu an.
Die potentielle Energie im Kasten ist gleich 0 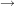 V=0. V=0.
Nun wir suchen also eine Funktion 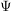 , die die Eigenschaft haben soll, dass wenn man sie zwei mal ableitet, soll die Funktion selbst mit einem Vorfaktor heraus kommen. Das nennt man dann periodische Funktionen. Ein Beispiel dafuer ist eine e-Funktion wie zum Beispiel , die die Eigenschaft haben soll, dass wenn man sie zwei mal ableitet, soll die Funktion selbst mit einem Vorfaktor heraus kommen. Das nennt man dann periodische Funktionen. Ein Beispiel dafuer ist eine e-Funktion wie zum Beispiel 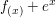 . Beim Ableiten kommt man wieder auf . Beim Ableiten kommt man wieder auf 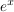 , der Vorfaktor hier waere also 1. Eine andere Moeglichkeit waere eine sinus oder cosinus Funktion. Wir versuchen das mal mit der sinus Funktion. Aber warum? , der Vorfaktor hier waere also 1. Eine andere Moeglichkeit waere eine sinus oder cosinus Funktion. Wir versuchen das mal mit der sinus Funktion. Aber warum?
Damti unsere Welle sich nicht durch Inteferenz selbst ausloescht muss es sich um eine stehende Welle handeln. Diese beginnt im Urspung (x=0) und endet bei x=L, um danach periodisch weiter zu laufen. In unserem Bezugssystem setzen wir also x in den Ursprung. Und genau diese Form hat auch eine sin-Funktion. Wenn wir unser Bezugssystem anders waehlen, so kann aber auch eine cos-Funktion in Frage kommen!
Eine allgemeine Wellengleichung koennte demnach durch folgende sin-Funktion beschrieben werden.
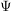 ist unsere Wellenfunktion. A der Normierungsfaktor (einfach eine Zahl, die wir spaeter noch genauer betrachten werden), b wieder ein Faktor (bis jetzt auch noch nicht sooo wichtig) und x die Ortskoordinate. ist unsere Wellenfunktion. A der Normierungsfaktor (einfach eine Zahl, die wir spaeter noch genauer betrachten werden), b wieder ein Faktor (bis jetzt auch noch nicht sooo wichtig) und x die Ortskoordinate.
Ok leiten wir diese Funktion zwei mal nach dem Ort ab kommen wir auf:
Dies setzen wir jetzt mal in unsere Schroedinger Gleichung ein.
ARTIKEL WIRD NOCH FORTGESETZT!!!
|