Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Dipl. math. Felix Fontein
Dipl. math. Dieter Osterholz | www.matheraum.de
Algebra-Training 2006
Aufgabenblatt 2
Abgabe: Fr 15.09.2006 12:00 | 08.09.2006 | | Aufgabe 6 | Sei X eine Menge, 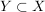 eine Teilmenge, G eine Gruppe und eine Teilmenge, G eine Gruppe und 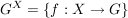 die Gruppe der G-wertigen Funktionen auf X. Sei die Gruppe der G-wertigen Funktionen auf X. Sei 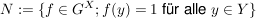 . Man zeige, daß N ein Normalteiler in . Man zeige, daß N ein Normalteiler in 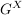 mit mit 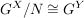 ist. ist. | | Aufgabe 7 | Sei G eine endliche Gruppe, 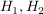 seien Untergruppen mit seien Untergruppen mit 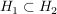 . Dann gilt . Dann gilt 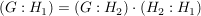 . . | | Aufgabe 8 | Eine Gruppe G enthalte einen Normalteiler N mit der folgenden Maximalitätseigenschaft: Ist 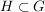 Untergruppe mit Untergruppe mit 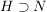 , so gilt bereits H = G oder H = N. Man zeige, daß je zwei Untergruppen , so gilt bereits H = G oder H = N. Man zeige, daß je zwei Untergruppen 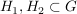 mit mit 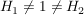 und und 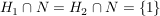 zueinander isomorph sind. zueinander isomorph sind. | | Aufgabe 9 | Sei 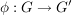 ein Gruppenhomomorphismus. Man zeige: ein Gruppenhomomorphismus. Man zeige:
(i) Ist 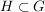 Untergruppe, so ist Untergruppe, so ist 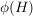 Untergruppe in Untergruppe in 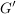 . Die entsprechende Aussage für Normalteiler ist allgemein nur dann richtig, wenn . Die entsprechende Aussage für Normalteiler ist allgemein nur dann richtig, wenn 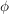 surjektiv ist. surjektiv ist.
(ii) Ist 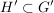 Untergruppe (bzw. Normalteiler) in Untergruppe (bzw. Normalteiler) in 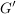 , so gilt dasselbe für , so gilt dasselbe für  . . |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|