Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Dipl. math. Felix Fontein
Dipl. math. Dieter Osterholz | www.matheraum.de
Algebra-Training 2006
Aufgabenblatt 3
Abgabe: Fr 22.09.2006 12:00 | 15.09.2006 | | Die Definition des cartesischen Produktes findet sich hier. | | Aufgabe 10 | Man betrachte 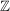 als additive Untergruppe von als additive Untergruppe von 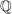 und zeige: und zeige:
i) Jedes Element in 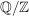 ist von endlicher Ordnung. ist von endlicher Ordnung.
ii) Für jedes 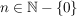 besitzt besitzt 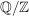 genau eine Untergruppe der Ordnung n, und diese ist zyklisch. genau eine Untergruppe der Ordnung n, und diese ist zyklisch. | | Aufgabe 11 | Es seien 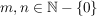 . Man zeige, daß die Gruppen . Man zeige, daß die Gruppen 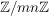 und und 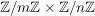 genau dann isomorph sind, wenn m und n teilerfremd sind. Insbesondere ist ein Produkt zweier zyklischer Gruppen mit teilerfremden Ordnungen wieder zyklisch. genau dann isomorph sind, wenn m und n teilerfremd sind. Insbesondere ist ein Produkt zweier zyklischer Gruppen mit teilerfremden Ordnungen wieder zyklisch.
(Das Produkt zweier Gruppen ist die Menge der geordneten Paare mit komponentenweiser Verknüpfung.) | | Aufgabe 12 | Es sei 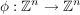 ein Endomorphismus des n-fachen Produkts der additiven Gruppe ein Endomorphismus des n-fachen Produkts der additiven Gruppe 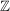 . Man zeige: . Man zeige: 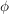 ist genau dann injektiv, wenn ist genau dann injektiv, wenn 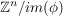 eine endliche Gruppe ist. eine endliche Gruppe ist.
(Hinweis: Man betrachte den zu 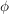 gehörigen Homomorphismus von gehörigen Homomorphismus von 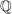 -Vektorräumen -Vektorräumen 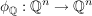 .) .) | | Aufgabe 13 | Seien G eine endliche Gruppe und S und T zwei (nicht notwendig verschiedene) Teilmengen von G. Dann gilt G = ST oder 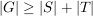 . .
In der Originalversion heißt es: Dann gilt entweder G = ST oder 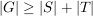 . Ist das auch richtig? . Ist das auch richtig?
Dabei ist 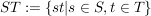 . ST ist selbst dann nicht unbedingt eine Untergruppe, wenn S und T es sind. . ST ist selbst dann nicht unbedingt eine Untergruppe, wenn S und T es sind. |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|