Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Dietlind Bäro
Daniel Metzsch | www.matheraum.de
Mathe für's ABI 2008
Aufgabenblatt 4
Abgabe: Mo 26.11.2007 20:00 | 12.11.2007 | | Aufgabe 1 | Zu jedem  ist eine Funktion ist eine Funktion 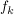 gegeben durch gegeben durch
 ; ;  . .
a. Bestimmen Sie die Schnittpunkte mit der t-Achse, die Hoch-, Tief- und Wendepunkte sowie die Asymptoten des Graphen von 
b. Begründen Sie, dass der folgende Graph zu  gehört. gehört.
![[Dateianhang]](uploads/forum/00208706/forum-i00208706-n001.png)
c. Die t-Achse und der Graph von 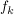 begrenzen eine bis ins Unendliche reichende Fläche. begrenzen eine bis ins Unendliche reichende Fläche.
Berechnen Sie die Gleichung der zur t-Achse senkrechten Geraden g, die diese
Fläche in zwei Teilflächen einteilt, sodass der Inhalt der linken Teilfläche dreimal so groß ist wie der Inhalt der rechten Teilfläche.
d. Der Graph von  (siehe Aufgabenteil b) zeigt den Verlauf einer Schädlingspopulation in einem Wald während der Bekämpfung mit einem Pestizid, beginnend bei (siehe Aufgabenteil b) zeigt den Verlauf einer Schädlingspopulation in einem Wald während der Bekämpfung mit einem Pestizid, beginnend bei  = 0 und endend zu der Zeit = 0 und endend zu der Zeit  , ab der keine Schädlinge im Wald mehr vorhanden sind. , ab der keine Schädlinge im Wald mehr vorhanden sind.
Dabei gilt Folgendes:
1 Einheit der Funktionswerte  1000 Schädlinge 1000 Schädlinge
1 Einheit der t-Werte  1 Tag 1 Tag
d1. Beschreiben Sie kurz den Verlauf der Population im Intervall ![$ [t_1;t_2]. $ $ [t_1;t_2]. $](/teximg/5/7/00478475.png) Gehen Sie dabei auf die Größe und auf die Wachstumsgeschwindigkeit der Schädlingspopulation ein. Gehen Sie dabei auf die Größe und auf die Wachstumsgeschwindigkeit der Schädlingspopulation ein.
d2. 18 Stunden bevor die Population am stärksten wuchs, wurde das Pestizid über dem Wald versprüht. Bestimmen Sie den Zeitpunkt und die Anzahl der Schädlinge zu diesem Zeitpunkt.
d3. Jeder Schädling vertilgt pro Tag 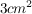 Blattfläche. Wie viel Blattfläche wurde von den Schädlingen insgesamt gefressen? Blattfläche. Wie viel Blattfläche wurde von den Schädlingen insgesamt gefressen?
|
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|