ÄhnlichkeitstransformationZustandsgrößen sind in einem n-dimensionalen Zustandsraum festgelegt. Eine Änderung der Größen bedeutet eine Änderung des Koordinatensystems. Dieses muss angepasst werden, damit der neue und alte Zustand konform bleiben.
Eine entsprechende Koordinatentransformation ist also eine Anpassung des Koordinatensystems gemäß der Zustandsänderung. Die neu entstandene Dynamikmatrix ist der ursprünglichen ähnlich. Die Ähnlichkeit bezieht sich auf den n-dimensionalen Raum (er wird beibehalten).
Die Determinante ist invariant, so dass gilt:
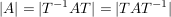
Hier ist T die Transformationsmatrix.
Des weiteren bleiben natürlich die Eigenwerte erhalten und es ist:
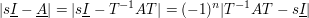
für eine n-reihige quadratische Matrix A.
Vor und nach der Transformation wird dasselbe System beschrieben.
Beispiel: Diagonalisierung
gegeben sei eine Matrix 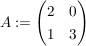
Für den Eigenvektor wird 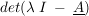 ermittelt: ermittelt:
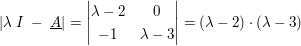
Die Eigenwerte lauten somit: 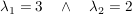
1. Eigenvektor
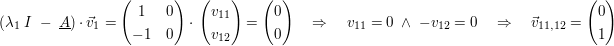
2. Eigenvektor

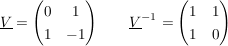
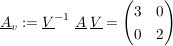
Diese Matrix 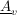 ist der obigen Matrix ist der obigen Matrix 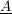 ähnlich. ähnlich.
zur Übersicht Regelungstechnik
|