AsymptoteDefinition Asymptote
Schule
Eine Funktion f hat eine Gerade als Asymptote, wenn sich der Graph von f
für 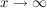 an diese Gerade annähert. an diese Gerade annähert.
Man unterscheidet zwischen waagerechten, senkrechten und schiefen Asymptoten. Es kann auch vorkommen, dass eine Funktion sich einer anderen Kurve nähert, in diesem Fall spricht man von einer Schmiegekurve.
Bestimmung von Asymptoten:
1. Konvergiert f für 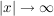 gegen eine Zahl a, d.h. gilt gegen eine Zahl a, d.h. gilt 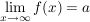 , dann ist die Gerade y=a eine waagerechte Asymptote der Funktion f. Für , dann ist die Gerade y=a eine waagerechte Asymptote der Funktion f. Für ist analog y=b eine waagerechte Asymptote. ist analog y=b eine waagerechte Asymptote.
Beispiel:
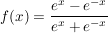
Es gilt 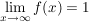 und und  . Damit ist y=1 waagerechte Asymptote für . Damit ist y=1 waagerechte Asymptote für  und y=-1 waagerechte Asymptote für und y=-1 waagerechte Asymptote für 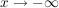 . .
2. Hat f die Polstelle  , d.h. gilt , d.h. gilt 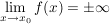 , dann hat die Funktion f die senkrechte Asymptote , dann hat die Funktion f die senkrechte Asymptote  . .
Beispiel:

Es gilt  , daher ist x=1 eine senkrechte Asymptote. , daher ist x=1 eine senkrechte Asymptote.
3. Gibt es eine Polynomfunktion p der sich f beliebig genau nähert, d.h. gilt 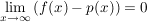 bzw. bzw. 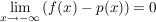 , dann ist p eine Schmiegekurve von f. Ist p eine lineare Funktion ( , dann ist p eine Schmiegekurve von f. Ist p eine lineare Funktion ( ) spricht man von einer schiefen Asymptote. ) spricht man von einer schiefen Asymptote.
Beispiel:
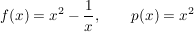
Wegen  ist p eine Schmiegekurve von f. ist p eine Schmiegekurve von f.
4. Für gebrochen-rationalen Funktionen gilt insbesondere:
Bei gebrochenrationalen Funktionen bestimmt man jeweils Grad des Zählers (Z) und Grad des Nenners (N).
Als "Grad" bezeichnet man die höchste vorkommende Hochzahl beim x.
Dann gilt:
Ist Z<N , dann gilt 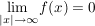 , also ist dann die x-Achse die waagrechte Asymptote. , also ist dann die x-Achse die waagrechte Asymptote.
Kann man auch rechnerisch nachweisen:
Erweitere einfach im Zähler und Nenner mit  , wobei Z der Zählergrad ist. Jetzt sieht man, nach dem Kürzen in Zähler und Nenner, dass der Zähler gegen eine konstante Zahl geht, und der Nenner , wobei Z der Zählergrad ist. Jetzt sieht man, nach dem Kürzen in Zähler und Nenner, dass der Zähler gegen eine konstante Zahl geht, und der Nenner 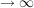 (oder (oder 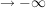 ), also der Bruchwert ), also der Bruchwert 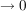 . .
Beispiel:  . .
Für 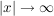 geht der Zähler geht der Zähler 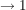 , der Nenner , der Nenner 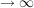 (wegen dem (wegen dem 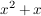 ), und somit der Bruchwert ), und somit der Bruchwert 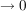 . .
Ist Z=N, so hat die Funktion eine waagerechte Asymptote, die nicht die x-Achse ist (also parallel dazu, eine Gerade der Form y=c).
Gegen welche waagerechte Asymptote das geht, siehst du an den Vorfaktoren des "höchsten x" in Zähler und Nenner. Wird klar am Beispiel.
Beispiel: 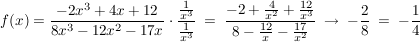 . .
Also braucht man im Fall Z=N nur die Koeffizienten vom "höchsten x" in Zähler und Nenner durcheinander zu dividieren, und hat eine waagerechte Asymptote, in meinem Beispiel also  . .
Gilt Z>N, so erhält man eine schiefe Asymptote, wenn Z um 1 größer ist als N, und eine asymptotische Kurve, wenn Z um 2 oder mehr größer ist als N.
Berechnung ist nicht schwer.
Polynomdivision Zähler:Nenner, der ganzrationale Anteil (also alles, wo kein x im Nenner steht) ist der Term für die schiefe Asymptote oder die asymptotische Kurve (Schmiegekurve).
Bemerkung:
Es gibt auch Schulbücher, die definieren:
Eine Polynomfunktion A(x) heißt Asymptote einer rationalen Funktion f(x) für 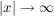 , wenn gilt: , wenn gilt:
Universität
|