Benutzer:tobit09/Beweis-Anleitung GrundsätzlichesWie führe ich einen Beweis?
 1. Einleitung 1. Einleitung  Inhaltsverzeichnis Inhaltsverzeichnis  3. Wie zeige ich...? 3. Wie zeige ich...?
2. Grundsätzliches zum Beweisen
Wie bereite ich einen Beweis vor?
Eigentlich eine Binsenweisheit, aber trotzdem von vielen nicht beachtet: Man kann kaum einen erfolgreichen Beweis führen, wenn man sich nicht klargemacht hat, was die Voraussetzungen und die Behauptung bedeuten. Rekapituliere also alle entsprechenden Definitionen bzw. schlage sie nach. Schreibe dir am besten für jede einzelne Voraussetzung und für die Behauptung auf, was sie bedeutet.
Falls eine Voraussetzung oder Behauptung beispielsweise "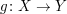 surjektiv" lautet, schreibe nicht surjektiv" lautet, schreibe nicht
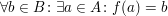
(also die Definition von "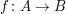 surjektiv") auf, sondern surjektiv") auf, sondern
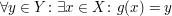 . .
Hier ein paar Beispiele von Aussagen, deren Bedeutung vielen nicht klar ist:
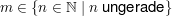
bedeutet: Es gilt 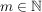 und und  ist ungerade. ist ungerade.
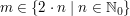
bedeutet: Es existiert ein 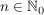 mit mit 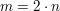 . (Beachte, dass der Existenzquantor in der Mengennotation nicht auftaucht!) . (Beachte, dass der Existenzquantor in der Mengennotation nicht auftaucht!)
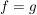 für zwei Abbildungen für zwei Abbildungen 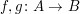
bedeutet: Für alle 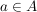 gilt gilt 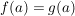 . .
Wie führe ich einen Beweis?
Du weißt also nun, was die Voraussetzungen und Behauptungen bedeuten. Einen Rahmen für deinen Beweis erhältst du, indem du unter 3. Wie zeige ich...? an der zu deiner Behauptung passenden Stelle nachschlägst, was zu tun ist. Eventuell heißt es dort wiederum "Zeige eine Aussage 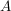 .". Dann gilt es, .". Dann gilt es, 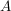 als neue Teilbehauptung zu betrachten und wieder an der passenden Stelle unter 3. Wie zeige ich...? nachzuschlagen. als neue Teilbehauptung zu betrachten und wieder an der passenden Stelle unter 3. Wie zeige ich...? nachzuschlagen.
Schreibe dabei immer wieder explizit auf, was eigentlich nun zu zeigen ist.
Nachdem der Rahmen für den Beweis steht, gilt es, den Hauptteil des Beweises auszufüllen. Suche nach Möglichkeiten, die Voraussetzungen anzuwenden. Lies dazu die passenden Stellen unter 4. Wie benutze ich...? nach. So gelangst du, wenn alles glatt geht, zu einer lückenlosen Folgerung der Behauptung.
|