Benutzer:tobit09/Beweis-Tutorial A15Beweis-Tutorial
 4. "für alle"-Aussagen 4. "für alle"-Aussagen
Lösungsvorschlag Aufgabe 15
Aufgabe:
Zeige, dass die Funktion 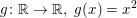 gerade ist. gerade ist.
Überlegungen zur Lösung:
Zu zeigen ist 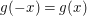 für alle reellen Zahlen für alle reellen Zahlen  . .
Wir betrachten also eine beliebig vorgegebene reelle Zahl 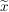 und wollen für diese Zahl und wollen für diese Zahl 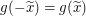 zeigen. zeigen.
Wegen 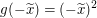 und und 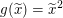 müssen wir also müssen wir also 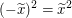 zeigen. Letzteres ist dir wahrscheinlich aus der Schule bekannt. zeigen. Letzteres ist dir wahrscheinlich aus der Schule bekannt.
Lösungsvorschlag:
Sei 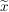 eine beliebig vorgegebene reelle Zahl. eine beliebig vorgegebene reelle Zahl.
Dann gilt 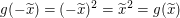 . .
Da 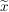 beliebig vorgegeben war, gilt somit beliebig vorgegeben war, gilt somit 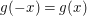 für alle reellen Zahlen für alle reellen Zahlen  . .
Also ist 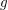 gerade. gerade.
|