BerührpunktEin Berührpunkt  ist ein Punkt, der auf den Graphen zweier Funktionen f und g liegt und an dem beide Graphen dieselbe (Tangenten)steigung haben.
Also gilt:  UND 
Sucht man Schnittstellen von f und g, zählt diese Schnittstelle doppelt, das heisst  ist eine doppelte Nullstelle von der Differenzfunktion
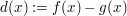
Eine dieser Funktionsgraphen kann natürlich auch die x-Achse sein.
Beispiel: f(x)=x² berührt die x-Achse (g(x)=0) im Ursprung O(0/0)
Beweis: f(0)=0, f'(0)=2*0=0 g(0)=0 und g'(0)=0
| 
