BruchtermGrundsätzliches
Das Rechnen mit Bruchtermen folgt den Regeln der Bruchrechnung mit reellen Zahlen.
Als Grundbedingung für die Variablen muss nur gelten, dass die Terme im Nenner jeweils nicht Null sein dürfen.
Addition und Subtraktion von gleichnamigen und ungleichnamigen Bruchtermen:
gleichnamige Brüche werden addiert, indem man die Zähler addiert und den Nenner beibehält.
ungleichnamige Brüche werden zunächst gleichnamig gemacht, dann kann man obige Regel anwenden.
Es gilt: 
Der Hauptnenner dieser Brüche ist also 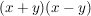
Der erste Bruch muss mit  erweitert werden, erweitert werden,
der zweite Bruch mit 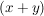 , der dritte muss nicht erweitert werden: , der dritte muss nicht erweitert werden:
Jetzt fasst man die Terme auf den Zählern zusammen und behält den Hauptnenner:
Natürlich kann man die Zähler noch weiter vereinfachen. (:lol:)
Multiplikation von Bruchtermen:
Brüche werden multipiziert, indem man die Zähler miteinander und die Nenner miteinander multipliziert.
Man erkennt sofort, dass in Zähler und Nenner gleiche Faktoren auftreten, daher sollte man vor dem Ausmultiplizieren erst kürzen und dabei beachten, dass 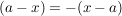 gilt. gilt.
Ergebnis daher:
Division von Bruchtermen:
Zwei Brüche werden dividiert, indem man den ersten mit dem Kehrbruch des zweiten multipliziert.
Auch hier kann man in Zähler und Nenner ausklammern und kürzen:
Kürzen von Bruchtermen:
Analog zum Kürzen von Bruchzahlen kann man auch Bruchterme kürzen, wenn sie im Zähler und im Nenner den identischen (Teil-)Term enthalten:
|