GruppenhomomorphismusDefinition Begriff
Universität
Die Definition bettet sich in die allgemeine Definition eines Homomorphismus einer algebraischen Struktur ein:
Es seien 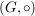 , , 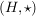 Gruppen. Eine Abbildung Gruppen. Eine Abbildung 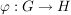 heißt ein (Gruppen-)Homomorphismus, wenn für alle heißt ein (Gruppen-)Homomorphismus, wenn für alle 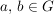 gilt: gilt:
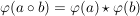 . .
Die Homomorphismen zwischen zwei Gruppen sind also genau die Abbildungen, welche die Gruppenstruktur "respektieren".
Beispiele
a) Die Exponentialabbildung auf 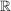 , , 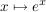 , ist wegen , ist wegen 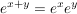 ein Homomorphismus von ein Homomorphismus von 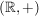 in in 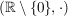 . .
b) Seien 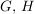 Gruppen und Gruppen und  das neutrale Element von das neutrale Element von  . Die Abbildung . Die Abbildung 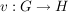 , definiert durch , definiert durch 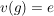 für alle für alle 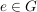 , ist ein Homomorphismus. , ist ein Homomorphismus.
c) Es sei 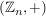 die additive Gruppe der Restklassen modulo die additive Gruppe der Restklassen modulo  . Dann ist . Dann ist 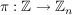 , definiert durch , definiert durch 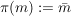 , , 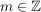 , auf Grund der Definition der Addition in , auf Grund der Definition der Addition in 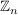 ein Homomorphismus. ein Homomorphismus.
Homomorphismen mit weiteren Eigenschaften erhalten besondere Namen:
Es seien 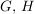 Gruppen und Gruppen und 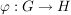 ein Homomorphismus. ein Homomorphismus.
a) 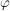 heißt ein Monomorphismus (bzw. Epimorphismus), wenn heißt ein Monomorphismus (bzw. Epimorphismus), wenn 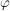 injektiv (bzw. surjektiv) ist. injektiv (bzw. surjektiv) ist.
b) 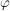 heißt ein Isomorphimus, wenn heißt ein Isomorphimus, wenn 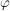 bijektiv ist. bijektiv ist.
c) Ein Homomorphismus von  in sich heißt ein Endomorphismus und ein Isomorphismus von in sich heißt ein Endomorphismus und ein Isomorphismus von  auf sich heißt Automorphismus. auf sich heißt Automorphismus.
d)  und und  heißen isomorph, in Zeichen heißen isomorph, in Zeichen 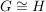 , wenn es einen Isomorphismus von , wenn es einen Isomorphismus von  auf auf  gibt. gibt.
Man weißt leicht nach, dass für einen Gruppemhomomorphismus 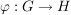 gilt: gilt:
![$ \varphi(a^n) = [\varphi(a)]^n $ $ \varphi(a^n) = [\varphi(a)]^n $](/teximg/2/4/00387842.png) für alle für alle 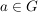 , , 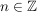 . .
Insbesondere gilt:
![$ \varphi(a^{-1}) = [\varphi(a)]^{-1} $ $ \varphi(a^{-1}) = [\varphi(a)]^{-1} $](/teximg/3/4/00387843.png) für alle für alle 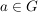
und 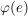 ist das neutrale Element von ist das neutrale Element von  , wenn , wenn  das neutrale Element von das neutrale Element von  ist. ist.
Man definiert weiterhin:
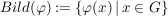
und
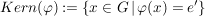 , ,
wenn 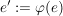 das neutrale Element von das neutrale Element von  ist. ist.
Während 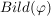 als "Maß für die Surjektivität" von als "Maß für die Surjektivität" von 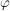 angesehen werden kann, "misst" angesehen werden kann, "misst" 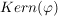 die Injektivität. Insbesondere gilt: die Injektivität. Insbesondere gilt:
Ein Gruppenhomomorphismus 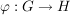 ist genau dann injektiv, wenn ist genau dann injektiv, wenn 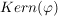 nur aus dem neutralen Element von nur aus dem neutralen Element von  besteht. besteht.
Siehe auch: Automorphismengruppe
Quelle: isbn3446130799
|