Hurwitz-DeterminanteHurwitz-Determinante
Um die Stabilität zu gewährleisten, müssen zum einen in dem Hurwitzpolynom:
1. alle Koeffizienten vorhanden sein
2. alle Koeffizienten gleiches Vorzeichen besitzen
Dieses Polynom n-ten Grades wird in einer Matrix folgendermaßen dargestellt:
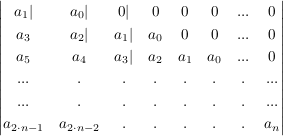
zum anderen
3. alle Hurwitz-Unterdeterminanten positiv sein.
Damit sind die Nord-Westwertigen Unterdeterminaten (angedeutet durch die kleinen Striche in der Determinante) gemeint.
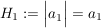
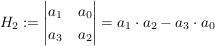
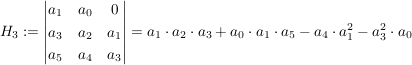
..
.
somit muss 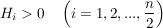 sein um das Stabilitätskriterium zu erfüllen. sein um das Stabilitätskriterium zu erfüllen.
zur Übersicht Regelungstechnik
|