IntervallDefinition Intervall
... heißt eine zusammenhängende Teilmenge der reellen Zahlen.
 nennt man ein abgeschlossenes Intervall nennt man ein abgeschlossenes Intervall
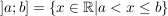 nennt man ein links-offenes Intervall nennt man ein links-offenes Intervall
Alternative Schreibweise: (a,b]
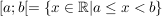 nennt man ein rechts-offenes Intervall nennt man ein rechts-offenes Intervall
Alternative Schreibweise: [a,b)
 nennt man ein offenes Intervall nennt man ein offenes Intervall
Alternative Schreibweise: (a,b)
Analog gilt für unbeschränkte Intervalle:

speziell: 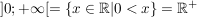 , , 
Universität
Intervalle können auch für den 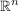 definiert werden: definiert werden:
Es seien 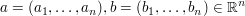 zwei Punkte des zwei Punkte des 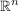 . Das Symbol " . Das Symbol "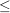 " sei im Zusammenhang " " sei im Zusammenhang " " definiert als " definiert als 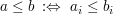 für alle für alle  . Entsprechend sei das Symbol " . Entsprechend sei das Symbol " " im Zusammenhang " " im Zusammenhang "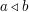 " definiert als: " definiert als: 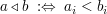 für alle für alle  . .
Intervalle im 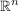 können dann folgendermaßen definiert werden: können dann folgendermaßen definiert werden:
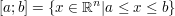 (abgeschlossenes Intervall) (abgeschlossenes Intervall)
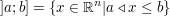 (nach links halboffenes Intervall) (nach links halboffenes Intervall)
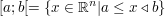 (nach rechts halboffenes Intervall) (nach rechts halboffenes Intervall)
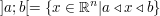 (offenes Intervall) (offenes Intervall)
Ein Intervall im 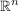 kann man sich also als einen achsenparallelen Quader vorstellen. kann man sich also als einen achsenparallelen Quader vorstellen.
Siehe auch: Elementarinhalt
|