KommutativgesetzKommutativgesetz:
In einer Summe oder einem Produkt darf man Summanden bzw. Faktoren vertauschen, wenn man die Vorzeichen der Summanden mitnimmt.
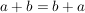
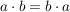
Kommutativgesetz der Addition:
In einer Summe darf man die Summanden vertauschen, wenn man dabei die Vorzeichen mitnimmt.
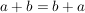
Beispiele:
a) 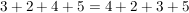
b) 
c) 
d) 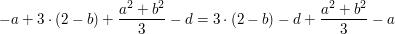
Man sieht also, dass man innerhalb einer Summe die einzelnen Summanden vertauschen kann, wenn man das Vorzeichen mitnimmt. Dabei können die Summanden durchaus auch verschiedene Terme sein.
Kommutativgesetz der Multiplikation:
In einem Produkt darf man die Faktoren vertauschen.
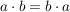
Beispiele:
a) 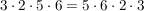
b) 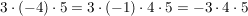
c) 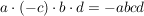
d) 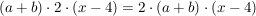
Bei den Beispielen ist aufgefallen, das das Vorzeichen an beliebiger Stelle im Produkt stehen kann. Da man 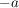 auch als auch als 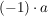 schreiben kann und dann für schreiben kann und dann für 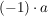 wieder das Kommutativgesetz gilt. wieder das Kommutativgesetz gilt.
siehe auch: Assoziativgesetz, Distributivgesetz, Rechengesetze
|