Laplace-VerschiebungssatzVerschiebungssätze
Eine Funktion 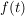 wird im Zeitbereich längs der t-Achse verschoben. Wir achten hier natürlich auf die Verschiebungsrichtung und betrachten daher die Auswirkung auf die Bildfunktion in zwei Fällen: wird im Zeitbereich längs der t-Achse verschoben. Wir achten hier natürlich auf die Verschiebungsrichtung und betrachten daher die Auswirkung auf die Bildfunktion in zwei Fällen:
1. Fall: die Verschiebung um den Wert  mit mit 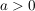
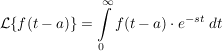
durch Substitution ergibt sich
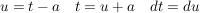
die Substitution hat folgende Auswirkung auf die Integrationsgrenzen
untere Grenze: 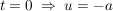
obere Grenze: 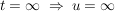
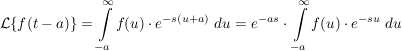
dieses Integral kann unterteilt werden im Intervall 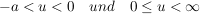
im ersten Intervallabschnitt ist es indentisch 0 und findet keine Berücksichtigung bei der weiteren Betrachtung, somit erhält man
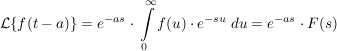
2.Fall: die Verschiebung um den Wert  mit mit 
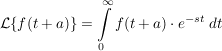
durch Substitution ergibt sich hier
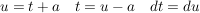
die Grenzen verändern sich entsprechend zu
untere Grenze: 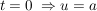
oberer Grenze: 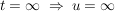
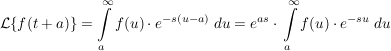
da das Intervall des Integrals im 2.Fall erst bei 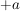 startet, aber bereits bei startet, aber bereits bei 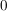 mit der Integration begonnen wird, muss der Wert des Intagrals im Teilintervall mit der Integration begonnen wird, muss der Wert des Intagrals im Teilintervall 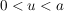 subtrahiert werden subtrahiert werden
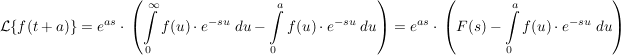
Für die Zusammenfassung ersetze ich wieder das  durch durch 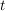 , um den Zeitbezug deutlich zu machen (bitte z.K.: diese Substitution hat aber nichts mit vorhergehnder zu tun). , um den Zeitbezug deutlich zu machen (bitte z.K.: diese Substitution hat aber nichts mit vorhergehnder zu tun).
erster Verschiebungssatz
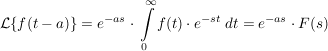
zweiter Verschiebungssatz
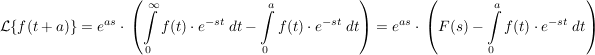
Beispiele folgen
zur Laplacetransformation
|