MaterialForum168
Gegliederte Aufgabe, die auch als mündliche Prüfungsaufgabe dienen könnte:
- Welches geometrische Gebilde wird durch die Funktion
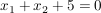 im im 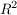 (also zweidimensionalen) und im (also zweidimensionalen) und im 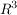 (also dreidimensionalen) dargestellt? (also dreidimensionalen) dargestellt?
- Gegeben ist die Funktion
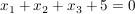 . Geben Sie die Hessesche Normalenform dieser Ebene an! . Geben Sie die Hessesche Normalenform dieser Ebene an!
- Geben Sie eine Parameterform dieser Ebene an!
- Welchen Abstand hat diese Ebene von Frage 2 vom Ursprung des Koordinatensystems?
- Geben Sie die Gleichung der kleinsten Kugel an, die durch den Ursprung geht und die die Ebene aus Frage 2 berührt.
(![Link auf "https://matheraum.de/read?t=154153" [link]](/images/popup.gif) zur Diskussion dieser Aufgabe) zur Diskussion dieser Aufgabe)
Geraden und Ebenen
Welche der Ebenen schneiden Ebene 4? Bestimme ggfs. die Schnittgeraden mit 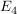 : :
Ebene 1: 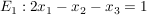
Ebene 2: 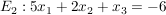
Ebene 3: 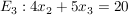
Ebene 4: 
(![Link auf "https://matheraum.de/read?t=153421" [link]](/images/popup.gif) zur Diskussion dieser Aufgabe) zur Diskussion dieser Aufgabe)
(a) Die Vektoren 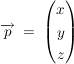 und und 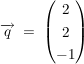 schliessen einen rechten Winkel ein. Der Vektor schliessen einen rechten Winkel ein. Der Vektor 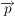 hat die Länge 15. Ferner gilt: hat die Länge 15. Ferner gilt: 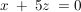 , mit , mit 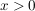 . .
Bestimmen Sie die Komponenten des Vektors 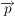 . .
(b) Mit den Vektoren 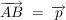 und und 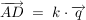 mit mit 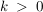 wird vom Punkt wird vom Punkt 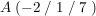 ein Quadrat ABCD aufgespannt. ein Quadrat ABCD aufgespannt.
Bestimmen Sie k und die Koordinaten der Eckpunkte B, C und D des Quadrates.
(c) Der Ursprung O ist die Spitze einer Pyramide mit der Grundfläche ABCD.
Berechnen Sie das Volumen der Pyramide.
(![Link auf "https://matheraum.de/read?t=165395" [link]](/images/popup.gif) zur Diskussion dieser Aufgabe) zur Diskussion dieser Aufgabe)
Kugeln
Es sei eine Kugel K, die alle Koordinatenebenen und die Ebene E: 2x + y - 2z = 5 berührt.
Begründen Sie, dass M(r|r|-r) als Kugelmittelpunkt gewählt werden kann.
(![Link auf "https://matheraum.de/read?t=367102" [link]](/images/popup.gif) zur Diskussion dieser Aufgabe: schöne Erklärung) zur Diskussion dieser Aufgabe: schöne Erklärung)
Gegeben sind die Punkte P(3|-3|4) und Q(3|0|7) der Grade g, sowie der Mittelpunkt M(7|1|6) der Kugel K. P liegt auf der Kugeloberfläche.
a) Wie groß ist der Radius der Kugel K?
b) Wie lang ist jene Strecke der Gerade g, die innerhalb der Kugel K verläuft.
(![Link auf "https://matheraum.de/read?i=381514" [link]](/images/popup.gif) zur Diskussion dieser Aufgabe) zur Diskussion dieser Aufgabe)
Ein Flugzeug A fliegt von der Position 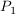 (6|-2|2) nach (6|-2|2) nach 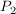 (-2|2|2). (-2|2|2).
Ein Flugzeug B fliegt von Position 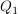 (2|3|1) nach (2|3|1) nach 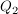 (-0,4|4|2,8). (-0,4|4|2,8).
a) Bestimmen Sie die kürzeste Entfernung der beiden Flugrouten.
b) Flugzeug A befindet sich zum selben Zeitpunkt an Position P1, wie Flugzeug B an Position Q1. Ihre Gleichschwindigkeit ist gleich.
Wie nah kommen sich beide Flugzeuge, wenn sie ihren Kurs jeweils bebehalten?
c) An welchem Ort tritt Flugzeug A in den Überwachungsraum einer im Punkt M(0|1|0) befindlichen Radarstation ein und wieder aus(Reichweite 3)?
(![Link auf "https://matheraum.de/read?t=384411" [link]](/images/popup.gif) zur Diskussion dieser Aufgabe) zur Diskussion dieser Aufgabe)
Welche Kugel mit dem Mittelpunkt auf der Geraden g: 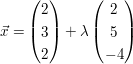 und dem Radius 9 und dem Radius 9
berührt die Ebene E: 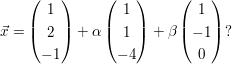
Bestimme den Berührungspunkt.
(![Link auf "https://matheraum.de/read?t=107132" [link]](/images/popup.gif) zur Diskussion dieser Aufgabe) zur Diskussion dieser Aufgabe)
Gegeben ist die Kugel K: (x+2)²+(y-5)²+(z-3)²=196, sowie die Ebene E: 2x+3y+6z=29
In einer vorhergehenden Teilaufgabe wurde bereits gezeigt, dass E die Kugel "halbiert" also durch den Mittelpunkt M (-2;5;3) verläuft.
Es gibt zwei Ebenen F und G, die parallel zu E verlaufen und die Kugel in Schnittkreisen mit dem Radius 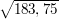 schneiden. Bestimmen Sie ihre Gleichungen! schneiden. Bestimmen Sie ihre Gleichungen!
(![Link auf "https://matheraum.de/read?t=371420" [link]](/images/popup.gif) zur Diskussion dieser Aufgabe) zur Diskussion dieser Aufgabe)
|