| Mach mit! und verbessere/erweitere diesen Artikel! | | Artikel • Seite bearbeiten • Versionen/Autoren | PartitionDefinition Partition
Schule
Universität
Es seien X, A Mengen. Eine Familie  von Teilmengen von X heißt eine Partition von X, wenn gilt: von Teilmengen von X heißt eine Partition von X, wenn gilt:
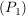 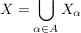 , ,
 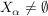 für alle für alle 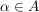 , ,
 aus aus  folgt folgt 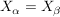  . .
Bemerkung
Jede Äquivalenzrelation R auf einer Menge X liefert eine Partition ![$ P(R) = \{[x]_R\}_{x \in X} $ $ P(R) = \{[x]_R\}_{x \in X} $](/teximg/1/1/00388011.png) . .
Quelle: isbn3446130799
| | Erstellt: Mi 20.07.2005 von Stefan | | Letzte Änderung: Mi 10.08.2005 um 23:54 von Stefan | | Weitere Autoren: Marc | | | Artikel • Seite bearbeiten • Versionen/Autoren • Titel ändern • Artikel löschen • Quelltext |
|