Primfaktorzerlegung
Schule
Eine natürliche Zahl 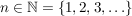 , die genau zwei unterschiedliche Teiler hat, heißt Primzahl. , die genau zwei unterschiedliche Teiler hat, heißt Primzahl.
Damit ist die Menge der Primzahlen: 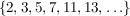 . .
Man erkennt, dass
- 1 nicht dazugehört, weil sie nur einen Teiler hat,
- 2 die einzige gerade Primzahl ist.
Jede beliebige natürliche Zahl lässt sich eindeutig in ein Produkt von Primzahlen zerlegen (Primfaktorzerlegung).
Beispiele siehe unten.
Universität
Satz Primfaktorzerlegung
Es sei n eine natürliche Zahl (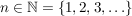 ). ).
Dann läßt sich n eindeutig (bis auf die Reihenfolge) als Produkt von Primzahlpotenzen darstellen.
Exakter: Zu der Menge der Primzahlen 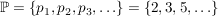 existiert eine eindeutig festgelegte Folge von Zahlen existiert eine eindeutig festgelegte Folge von Zahlen 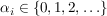 so dass gilt: so dass gilt:
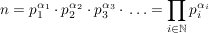
Diese Darstellung der Zahl n heißt Primfaktorzerlegung.
Bemerkungen.
Unter der (unendlich langen) Folge der 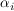 sind nur endlich viele Zahlen ungleich Null. sind nur endlich viele Zahlen ungleich Null.
Der ![Link auf "https://matheraum.de" [link]](/images/popup.gif) MatheRaum stellt ein MatheRaum stellt ein ![Link auf "https://matheraum.de/werkzeuge?werkzeug=primfaktorzerlegung" [link]](/images/popup.gif) Werkzeug zur Berechnung der Primfaktorzerlegung zur Verfügung. Werkzeug zur Berechnung der Primfaktorzerlegung zur Verfügung.
Beispiele.
1.) n=35; ![Link auf "https://matheraum.de/werkzeuge?werkzeug=primfaktorzerlegung&input=35" [link]](/images/popup.gif) Primfaktorzerlegung: Primfaktorzerlegung: 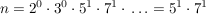
2.) n=144; ![Link auf "https://matheraum.de/werkzeuge?werkzeug=primfaktorzerlegung&input=144" [link]](/images/popup.gif) Primfaktorzerlegung: Primfaktorzerlegung: 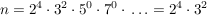
3.) n=1; ![Link auf "https://matheraum.de/werkzeuge?werkzeug=primfaktorzerlegung&input=1" [link]](/images/popup.gif) Primfaktorzerlegung: Primfaktorzerlegung: 
Beweis.
TODO
|