ProduktregelDie Ableitung einer differenzierbaren Funktion  an der Stelle an der Stelle  ist durch ist durch
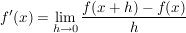
gegeben. Daher gilt für zwei an einer Stelle  differenzierbare Funktionen differenzierbare Funktionen  und und  : :
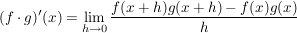 , ,
falls der Grenzwert auf der rechten Seite existiert.
Um die Produktregel
zu beweisen, müssen wir also zeigen, dass 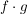 wieder an einer Stelle wieder an einer Stelle  differenzierbar ist (und damit die Existenz des Grenzwertes differenzierbar ist (und damit die Existenz des Grenzwertes 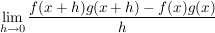 zeigen) und dann die Gleichheit zeigen) und dann die Gleichheit

beweisen.
Hierbei dürfen wir ausnutzen, dass
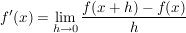
und
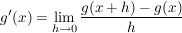
gilt.
siehe auch: ![Link auf "http://sites.inka.de/picasso/Simon/prdregel.html" [link]](/images/popup.gif) Produktregel Produktregel
|