TeilmengeDefinition Teilmenge
Schule
Definition Teilmenge
Gegeben ist eine Menge  .
Eine Menge 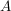 heißt Teilmenge von M, wenn jedes Element aus 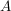 auch in  enthalten ist.
Man schreibt dann: 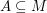 .
Definition echte Teilmenge
Gegeben ist eine Menge  .
Eine Menge 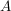 heißt echte Teilmenge von M, wenn 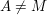 und jedes Element aus 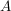 auch in  enthalten ist.
Man schreibt dann: 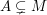 .
Die Menge  und die leere Menge und die leere Menge 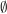 sind damit ebenfalls Teilmengen von sind damit ebenfalls Teilmengen von  : Es gilt : Es gilt 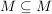 und und  . Allerdings ist . Allerdings ist  natürlich keine echte Teilmenge von natürlich keine echte Teilmenge von  . .
Häufige Verwendung findet auch das Symbol 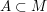 . Leider ist seine Bedeutung von Autor zu Autor unterschiedlich. Bei manche Autoren bedeutet . Leider ist seine Bedeutung von Autor zu Autor unterschiedlich. Bei manche Autoren bedeutet 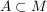 "A ist Teilmenge von M" (also "A ist Teilmenge von M" (also 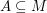 ), bei anderen Autoren bedeutet ), bei anderen Autoren bedeutet 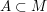 "A ist echte Teilmenge von M" (also "A ist echte Teilmenge von M" (also 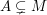 ). Im Allgemeinen wird aber die Bedeutung von ). Im Allgemeinen wird aber die Bedeutung von 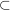 von jedem Autor angegeben. von jedem Autor angegeben.
Beispiele für Teilmengen
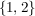 ist Teilmenge von ist Teilmenge von 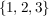 , in Zeichen: , in Zeichen: 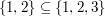 . .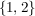 ist echte Teilmenge von ist echte Teilmenge von 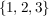 , in Zeichen: , in Zeichen:  . .
Universität
Fasst man Teilmengen einer Menge  wieder zu einer Menge zusammen, so erhält man ein Mengensystem von wieder zu einer Menge zusammen, so erhält man ein Mengensystem von  . .
Fasst man alle Teilmengen einer Menge  wieder zu einer Menge zusammen, so erhält man die Potenzmenge von wieder zu einer Menge zusammen, so erhält man die Potenzmenge von  . .
|