Typische Surjektivitäts- und Injektivitätssätze
Surjektivität
Satz S1 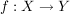 ist genau dann surjektiv, wenn für beliebige Mengen Z und beliebige Abbildungen 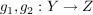 aus 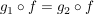 die Beziehung 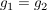 folgt.
siehe auch diese Diskussionen im ![Link auf "https://matheraum.de" [link]](/images/popup.gif) MatheRaum: MatheRaum: ![Link auf "https://matheraum.de/read?t=23485" [link]](/images/popup.gif) Diskussion Diskussion
Satz S2 Seien 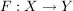 und 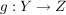 Abbildungen.
Zeigen Sie, dass 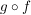 surjektiv ist, wenn 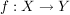 und 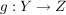 surjektiv sind.
("Die Komposition surjektiver Abbildungen ist surjektiv.")
siehe auch diese Diskussionen im ![Link auf "https://matheraum.de" [link]](/images/popup.gif) MatheRaum: MatheRaum: ![Link auf "https://matheraum.de/read?t=23754" [link]](/images/popup.gif) Diskussion Diskussion
Injektivität
siehe auch diese Diskussionen im ![Link auf "https://matheraum.de" [link]](/images/popup.gif) MatheRaum: MatheRaum: ![Link auf "https://matheraum.de/read?t=23485" [link]](/images/popup.gif) Diskussion Diskussion
Satz I2 Seien 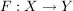 und 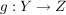 Abbildungen.
Zeigen Sie, dass 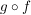 injektiv ist, wenn 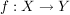 und 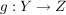 injektiv sind.
("Die Komposition injektiver Abbildungen ist injektiv.")
siehe auch diese Diskussionen im ![Link auf "https://matheraum.de" [link]](/images/popup.gif) MatheRaum: MatheRaum: ![Link auf "https://matheraum.de/read?t=23754" [link]](/images/popup.gif) Diskussion Diskussion
Bijektivität
Satz B2 Seien 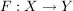 und 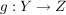 Abbildungen.
Zeigen Sie, dass 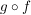 bijektiv bijektiv ist, wenn 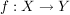 und 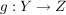 bijektiv sind.
Falls 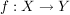 und 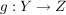 bijektiv sind, zeigen Sie zudem, dass gilt 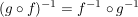 .
("Die Komposition bijektiver Abbildungen ist bijektiv.")
siehe auch diese Diskussionen im ![Link auf "https://matheraum.de" [link]](/images/popup.gif) MatheRaum: MatheRaum: ![Link auf "https://matheraum.de/read?t=23754" [link]](/images/popup.gif) Diskussion Diskussion
Beweise
Beweis von Satz S1 (![Link auf "https://matheraum.de/~marc" [link]](/images/popup.gif) Marc O. Sandlus) Marc O. Sandlus)
" " "
Sei 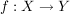 surjektiv und es seien surjektiv und es seien 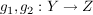 zwei beliebige Abbildungen mit zwei beliebige Abbildungen mit 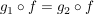 . .
Zu zeigen ist nun, dass 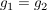 folgt. folgt.
Indirekter Beweis: Angenommen, 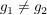 . Dann gibt es ein . Dann gibt es ein 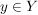 mit mit 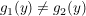 . .
Wegen der Surjektivität von f gibt es zu y ein 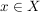 mit f(x)=y. Für dieses x gilt nun nach Voraussetzung mit f(x)=y. Für dieses x gilt nun nach Voraussetzung 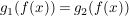 , also auch , also auch 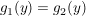 . Widerspruch! . Widerspruch!
"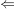 " "
Sei 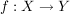 und es folge für beliebige Abbildungen und es folge für beliebige Abbildungen 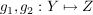 aus aus 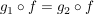 die Beziehung die Beziehung 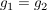 . .
Zu zeigen ist, dass f surjektiv ist.
Indirekter Beweis: Sei 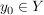 . Angenommen, f wäre nicht surjektiv. Dann existiert kein . Angenommen, f wäre nicht surjektiv. Dann existiert kein 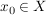 mit mit 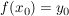 . .
Definiere nun 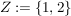 und zwei Abbildungen und zwei Abbildungen 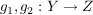 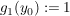 , , 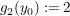 und und 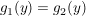 für alle für alle 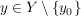 (die beiden Abbildungen stimmen also bis auf die Stelle (die beiden Abbildungen stimmen also bis auf die Stelle 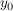 überein.) überein.)
Damit gilt 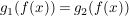 für alle für alle 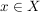 (da der Wert (da der Wert 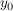 ja nicht von f angenommen wird), und nach Voraussetzung folgt nun ja nicht von f angenommen wird), und nach Voraussetzung folgt nun 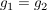 . Widerspruch (zur Konstruktion von . Widerspruch (zur Konstruktion von 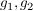 ). ).
Beweis von Satz I2 (![Link auf "https://matheraum.de/~stefan" [link]](/images/popup.gif) Stefan Hartmann) Stefan Hartmann)
Es seien also  und und 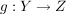 zwei injektive Abbildungen. Zu zeigen ist, dass dann auch zwei injektive Abbildungen. Zu zeigen ist, dass dann auch 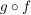 injektiv ist. injektiv ist.
Dazu seien 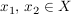 gewählt mit gewählt mit
(*) 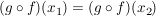 . .
Zu zeigen ist:
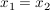 . .
Die Gleichung (*) bedeutet aber gerade:
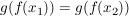 . .
Da g injektiv ist, folgt daraus:
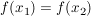 . .
Da aber auch 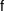 injektiv ist, ergibt sich injektiv ist, ergibt sich
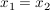 , ,
was zu zeigen war.
Beweis von Satz S2 (![Link auf "https://matheraum.de/~stefan" [link]](/images/popup.gif) Stefan Hartmann) Stefan Hartmann)
Es seien also  und und 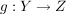 zwei surjektive Abbildungen. Zu zeigen ist, dass dann auch zwei surjektive Abbildungen. Zu zeigen ist, dass dann auch 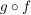 surjektiv ist. surjektiv ist.
Dazu seien 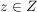 beliebig gewählt. Zu zeigen ist: Es gibt eine beliebig gewählt. Zu zeigen ist: Es gibt eine  mit mit
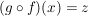 . .
Da g surjektiv ist, gibt es aber ein 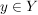 mit mit
g(y)=z.
Da f surjektiv ist, gibt es weiterhin ein  mit mit
f(x)=y.
Ingesamt gibt es also ein  mit mit
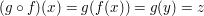 , ,
was zu zeigen war.
Beweis von Satz B2 (![Link auf "https://matheraum.de/~stefan" [link]](/images/popup.gif) Stefan Hartmann) Stefan Hartmann)
Sind nun 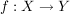 und und 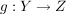 beide bijektiv, dann ist nach den Sätzen I2 und S2 auch beide bijektiv, dann ist nach den Sätzen I2 und S2 auch 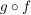 bijektiv. bijektiv.
Weiterhin gilt:
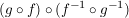
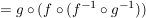

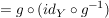
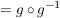
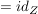 , ,
woraus die Behauptung
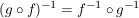
folgt.
|