Vektorraum
Universität
Es sei 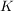 ein Körper. Ein ein Körper. Ein 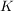 -Vektorraum (man sagt auch: ein Vektorraum über -Vektorraum (man sagt auch: ein Vektorraum über 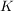 ) ist eine Menge ) ist eine Menge  mit einer Abbildung mit einer Abbildung 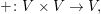 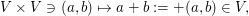 genannt Addition (auf genannt Addition (auf  ), sowie einer weiteren Abbildung ), sowie einer weiteren Abbildung 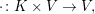 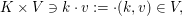 genannt skalare Multiplikation (oft auch, in etwas ungünstiger Weise als Skalarmultiplikation bezeichnet), so dass folgendes gilt: genannt skalare Multiplikation (oft auch, in etwas ungünstiger Weise als Skalarmultiplikation bezeichnet), so dass folgendes gilt:
(i) 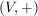 ist eine abelsche Gruppe, d.h. es gelten ist eine abelsche Gruppe, d.h. es gelten
(i,a): 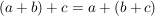 für alle für alle 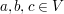 (Assoziativität) (Assoziativität)
(i,b): Es existiert ein 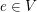 mit mit 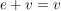 für alle für alle  (Existenz eines (links-)neutralen Elements) (Existenz eines (links-)neutralen Elements)
(i,c): Für alle  existiert ein existiert ein 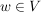 mit mit 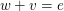 (Existenz (links-)inverser Elemente) (Existenz (links-)inverser Elemente)
(i,d): Für alle 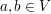 gilt gilt 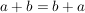 (Kommutativität) (Kommutativität)
(ii) 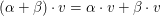 und und 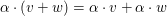 für alle für alle 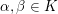 und und 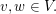 ("Distributivität") ("Distributivität")
(iii) 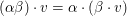 für alle für alle 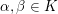 und und 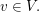 ("Assoziativät") ("Assoziativät")
(iv) 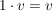 für alle für alle 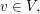 wobei wobei  das multiplikative Inverse in das multiplikative Inverse in 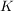 sei. sei.
Bemerkungen:
(1) In (iii) steht 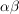 für für 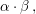 wobei hier allerdings wobei hier allerdings  die Multiplikation in die Multiplikation in 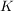 gemeint ist! gemeint ist!
(2) In (nicht notwendig abelschen) Gruppen gibt es genau ein links-neutrales Element, ebenso sind die links-inversen Elemente eindeutig. Ferner ist dann das linksneutrale Element auch rechtsneutral, und wird dann als das neutrale Element bezeichnet. Man spricht dann (in obigem Falle) auch von der additiven Null, und schreibt auch 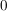 (bzw. oben auch (bzw. oben auch 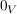 ) dafür. Das für ) dafür. Das für  eindeutig bestimmte (additiv) Inverse Element (links-inverse sind auch rechts-inverse Elemente und eindeutig) eindeutig bestimmte (additiv) Inverse Element (links-inverse sind auch rechts-inverse Elemente und eindeutig) 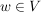 mit mit 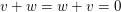 wird auch also wird auch also 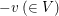 notiert: notiert: 
(3) In Körpern 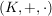 ist bekanntlich ist bekanntlich 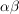 (wobei (wobei 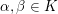 ) eine Kurznotation für ) eine Kurznotation für 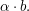 Analog schreiben wir auch bei der skalaren Multiplikation oben Analog schreiben wir auch bei der skalaren Multiplikation oben 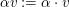 für für 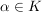 und und 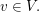
|