ZahlsystemeRechnen in anderen Zahlsystemen
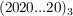 bezeichne die im Dreiersystem aus n Ziffernblöcken "20" dargestellte Zahl. bezeichne die im Dreiersystem aus n Ziffernblöcken "20" dargestellte Zahl.
Beweisen Sie: 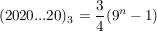
Die Ziffernfolge 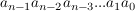 zur Basis zur Basis 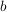 stellt ja diesen Wert dar: stellt ja diesen Wert dar:
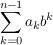
In diesem Beispiel ist 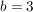 , die , die 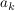 mit geradem mit geradem 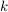 haben den Wert Null, die anderen den Wert haben den Wert Null, die anderen den Wert 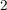 . .
Somit erhalten wir:
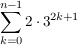
Von nun an sind es ganz einfache, elementare Umformungen:

Das ist die Summe der ersten n Glieder einer ![Link auf "http://de.wikipedia.org/wiki/Geometrische_Reihe" [link]](/images/popup.gif) Geometrischen Reihe. Geometrischen Reihe.
Dafür gibt es eine Formel: 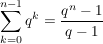
Somit weiter:
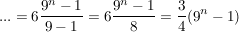
zur geometrischen Reihe siehe ![Link auf "http://de.wikipedia.org/wiki/Geometrische_Reihe" [link]](/images/popup.gif) Wikipedia Wikipedia
|