teilerfremdZwei (oder mehrere) natürliche Zahlen m und n heißen teilerfremd zueinander, wenn der Durchschnitt der Teilermengen der beiden Zahlen nur die 1 enthält.
Beispiel 1:
m=15 und n=28 sind teilerfremd, denn
 und und 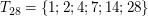
Damit dann

Beispiel 2:
m=18 und n=45 sind nicht teilerfremd, denn  und und 
Damit dann:

Die größte Zahl, die in der Schnittmenge zweier Teilermengen enthalten ist, nennt man den grössten gemeinsamen Teiler, kurz ggT.
Daher ist auch folgende Definition für teilerfremde Zahlen gebräuchlich.
Zwei natürliche Zahlen m und n heißen teilerfremd zueinander, wenn der ggT der beiden Zahlen 1 ist.
|