Argumentbestimmung komplexer ZahlenDie Argumentbestimmung komplexer Zahlen der Form 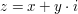 kann anhand nachfolgend aufgeführten Ansätzen erfolgen: kann anhand nachfolgend aufgeführten Ansätzen erfolgen:

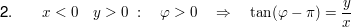
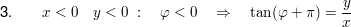
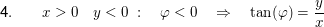
Der Hauptwert liegt immer zwischen 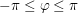 bzw. bzw. 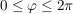
Beispiele
Zu 1. 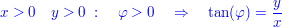

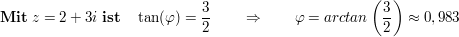
Zu 2. 
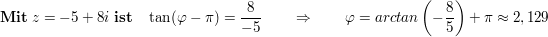
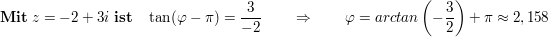
Zu 3. 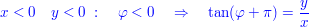


Zu 4. 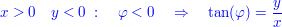
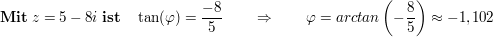

Weitere Anmerkungen
Alle Winkelangaben erfolgten in der Einheit "RAD". Für die Umrechnung des Winkels 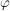 in "DEG" besteht die Beziehung: in "DEG" besteht die Beziehung:

Sollte generell ein positiver Drehwinkel gefordert sein, so ist der Wert  bzw. 360° zu den negativen Argumenten zu addieren. bzw. 360° zu den negativen Argumenten zu addieren.
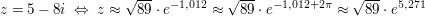
Übersicht MatheBank
|