komplexe ZahlMenge
Die Menge der komplexen Zahlen 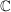 ist ganz abstrakt die Menge aller Paare von reellen Zahlen: ist ganz abstrakt die Menge aller Paare von reellen Zahlen:
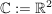
Zum Beispiel könnte das Zahlenpaar 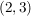 als eine komplexe Zahl aufgefasst werden. als eine komplexe Zahl aufgefasst werden.
Sehr verbreitet für die Schreibweise einer komplexen Zahl 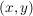 ist auch die kartesische oder algebraische Darstellung ist auch die kartesische oder algebraische Darstellung
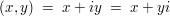
oder als Mengenbeschreibung
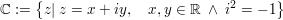
Zunächst sind dabei die Zeichen 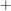 und und 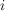 nur Symbole ohne jede Bedeutung, gewissermaßen "Trennzeichen" zwischen nur Symbole ohne jede Bedeutung, gewissermaßen "Trennzeichen" zwischen  und und  . Man sollte sie nicht sofort als Rechenzeichen "+" oder als Variable "i" auffassen. Später (bei Behandlung der definierten Verknüpfungen) wird sich aber zeigen, dass sich mit dieser Schreibweise die Verknüpfungsregeln sehr einfach merken lassen. . Man sollte sie nicht sofort als Rechenzeichen "+" oder als Variable "i" auffassen. Später (bei Behandlung der definierten Verknüpfungen) wird sich aber zeigen, dass sich mit dieser Schreibweise die Verknüpfungsregeln sehr einfach merken lassen.
Verknüpfungen
Es seinen nun 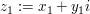 und und 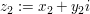 zwei komplexe Zahlen. In diesem Abschnitt sollen Verknüpfungen wie die Addition zwei komplexe Zahlen. In diesem Abschnitt sollen Verknüpfungen wie die Addition 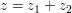 und Multiplikation und Multiplikation 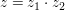 komplexer Zahlen definiert werden. komplexer Zahlen definiert werden.
Addition
In der Addition werden komplexe Zahlen folgendermaßen beschrieben:
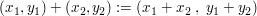
- Komplexe Zahlen werden also komponentenweise addiert. In der alternativen Darstellung sieht dies so aus:
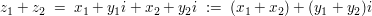
Multiplikation
Auf den ersten Blick vielleicht nicht ganz so naheliegend ist eine Multiplikation definiert durch
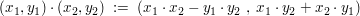
- Zum Vergleich wieder die kartesische Darstellung:
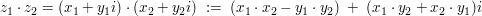
Diese Definition ist leicht zu merken, wenn man sich "naiv" nur merkt, dass 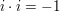 , denn dann sieht das Ergebnis der Multiplikation so aus, als wäre es durch formales ausmultiplizieren entstanden: , denn dann sieht das Ergebnis der Multiplikation so aus, als wäre es durch formales ausmultiplizieren entstanden:
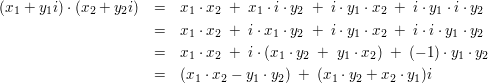
In dieser Vereinfachung des "Merkaufwands" liegt der Nutzen und die Bedeutung der kartesischen Schreibweise, die in diesem Artikel fortan verwendet wird.
Man kann leicht zeigen, dass beide Verknüpfungen assoziativ und kommutativ sind:
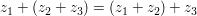 (Assoziativität der Addition) (Assoziativität der Addition)
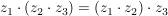 (Assoziativität der Multiplikation) (Assoziativität der Multiplikation)
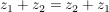 (Kommutativität der Addition) (Kommutativität der Addition)
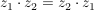 (Kommutativität der Multiplikation) (Kommutativität der Multiplikation)
Außerdem gilt das Distributivgesetz:
Beispiele für die Verknüpfungen
Körper
Zeigt man noch die Existenz der neutralen Elemente für die Addition und Multiplikation und die Existenz inverser Elemente, so gelten alle Körperaxiome.
Motivation für die Einführung der komplexen Zahlen
Die Polynomgleichung 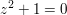 , die über den reellen Zahlen nicht lösbar ist, hat nun die beiden komplexzahligen Lösungen , die über den reellen Zahlen nicht lösbar ist, hat nun die beiden komplexzahligen Lösungen 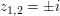 . Daher lässt sich der Term . Daher lässt sich der Term 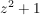 nun als Produkt in der "Linearfaktorschreibweise" darstellen: nun als Produkt in der "Linearfaktorschreibweise" darstellen: 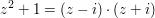 . Nach dem Fundamentalsatz der Algebra zerfällt sogar jedes Polynom vom Grad n in n Linearfaktoren. . Nach dem Fundamentalsatz der Algebra zerfällt sogar jedes Polynom vom Grad n in n Linearfaktoren.
Weitere Definitionen
- Komplex-Konjugiertes zu
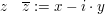
- Realteil zu
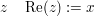
- Imaginärteil zu
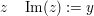
- Betrag von
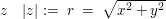
- Argument von
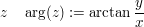
Umrechnung in die trigonometrische Form
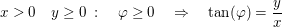
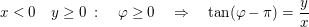
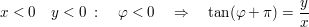
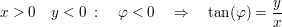
Konkrete Beispiele: Argumentbestimmung komplexer Zahlen
Umrechnung von der trigonometrischen Form in die Normalform
Für 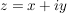 berechnet sich der Realteil berechnet sich der Realteil 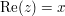 durch durch
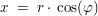
und der Imaginärteil 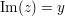 durch durch
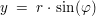
Exponentialform einer komplexen Zahl
Mit der Euler'schen Identität 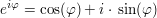 folgt für eine komplexe Zahl folgt für eine komplexe Zahl 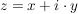
![$ z\ =\ r\cdot{}e^{i\cdot{}\varphi}\ =\ r\cdot{}\left[\cos(\varphi)+i\cdot{}\sin(\varphi)\right] $ $ z\ =\ r\cdot{}e^{i\cdot{}\varphi}\ =\ r\cdot{}\left[\cos(\varphi)+i\cdot{}\sin(\varphi)\right] $](/teximg/2/6/01314762.png)
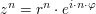 für für 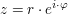
Rechnen mit der trigonometrischen Form
Es seien 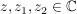 mit mit 
![$ \bruch{z_1}{z_2}=\bruch{r_1}{r_2}\cdot{}[\cos(\varphi_1-\varphi_2)+i\cdot{}\sin(\varphi_1-\varphi_2)] $ $ \bruch{z_1}{z_2}=\bruch{r_1}{r_2}\cdot{}[\cos(\varphi_1-\varphi_2)+i\cdot{}\sin(\varphi_1-\varphi_2)] $](/teximg/7/4/01314747.png) mit mit 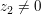
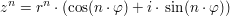 für für 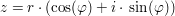
Zur Berechnung der Potenzen verwendet man i.a.R die Formel von Moivre-Laplace.
Rechenregeln für 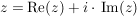
 ("Konjugiertenbildung ist verträglich mit der Addition") ("Konjugiertenbildung ist verträglich mit der Addition")
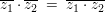 ("Konjugiertenbildung ist verträglich mit der Multiplikation") ("Konjugiertenbildung ist verträglich mit der Multiplikation")
Weitere Artikel bezüglich komplexer Zahlen
|