PolynomdivisionDie Polynomdivision ist, wie der Name sagt, ein Verfahren zur Division von Polynomen.
Dabei wird ein Term der Form
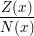
mit einem Zählerpolynom Z(x) und einem Nennerpolynom N(x) - wobei der Grad von N(x) kleiner
oder gleich dem von Z(x) sein soll - schrittweise umgeformt zu einem Ergebnis der Form
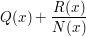
mit Polynomen Q(x) und R(x), wobei der Grad von R(x) kleiner ist als jener von N(x).
Anwendungen:
Untersuchung von gebrochen-rationalen Funktionen
Die Polynomdivision dient zur Bestimmung der Asymptoten oder asymptotischen Kurven der Funktion
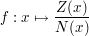
Die Funktion 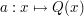 beschreibt das asymptotische Verhalten der Funktion für beschreibt das asymptotische Verhalten der Funktion für 
Ist Q(x)=const. , hat man eine horizontale Asymptote. Ist Q(x) linear, hat man eine geradlinige,
schräge Asymptote. Die Analyse des Terms 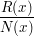 ermöglicht die Beschreibung des Verhaltens ermöglicht die Beschreibung des Verhaltens
der gegebenen gebrochen-rationalen Funktion in den Umgebungen von deren allfälligen Polstellen.
Auch bei der Integration von gebrochen-rationalen Funktionen leistet die Polynomdivision - in Verbindung
mit der Partialbruchzerlegung wichtige Dienste.
Polynomdivision als Verfahren zum Lösen von Gleichungen höheren Grades.
Angenommen, es liege eine Gleichung vor, deren linke Seite ein Polynom und deren rechte Seite Null ist:
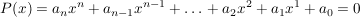
Falls sie n Lösungen 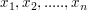 besitzt, kann sie nach dem Wurzelsatz von Vietá als Produkt von besitzt, kann sie nach dem Wurzelsatz von Vietá als Produkt von
Linearfaktoren gedacht werden:
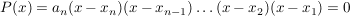
Auch wenn nicht die maximale Anzahl n an Lösungen vorliegt und z.B. nur eine Lösung  bekannt ist, bekannt ist,
kann das Polynom P(x) faktorisiert werden:
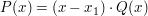
wobei das Polynom Q(x) einen um Eins niedrigeren Grad als P(x) hat.
Wenn eine Lösung  bekannt ist oder z.B. durch Probieren gefunden wurde, findet die Polynomdivision bekannt ist oder z.B. durch Probieren gefunden wurde, findet die Polynomdivision
Anwendung, um den Grad der Gleichung um Eins zu senken.
Durchführung
(für die Auflösung einer Polynomgleichung mit der bekannten Lösung  ) )
- Aus der Lösung
 wird der Linearfaktor wird der Linearfaktor 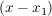 gebildet. gebildet.
- Die Divisionsaufgabe
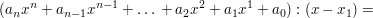
wird aufgestellt.
- Ähnlich wie bei der schriftlichen Division im Wesentlichen nur die erste Ziffer betrachtet wird,
muss hier darauf geachtet werden, dass jeweils die höchste Potenz von x vollständig aufgelöst
wird, unabhängig davon, was im Anschluss folgt. Wegen

beginnt das Ergebnis mit 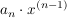 , also hat sich der Grad des Polynoms um Eins erniedrigt. (In der , also hat sich der Grad des Polynoms um Eins erniedrigt. (In der
Praxis wird bei der Nullstellensuche zu Beginn in einem Zwischenschritt die gesamte Gleichung durch 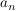
dividiert, da diese Konstante die Lösung nicht beeinflusst).
Der Quotient wird mit (x-xn) multipliziert und vom Dividenden abgezogen.
- Es wird solange die jeweils höchste x-Potenz wie im vorigen Schritt eliminiert, bis der Rest verschwindet.
Letzteres muss der Fall sein, falls  tatsächlich eine Nullstelle des Polynoms ist. tatsächlich eine Nullstelle des Polynoms ist.
Bei der allgemeineren Polynomdivision (bei der Untersuchung einer gebrochen-rationalen Funktion) fährt man
fort, bis der Grad des Restes R(x) den Grad des Divisorpolynoms N(x) um mindestens Eins unterschreitet.
Anwendungsbeispiel
Angenommen, die Gleichung
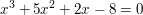
ist zu lösen und durch Probieren haben wir eine erste Lösung x=1 gefunden. Wir bilden das Binom (x-1) und schreiben:
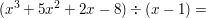
Da x³ : x = x² ergibt, entsteht hinter dem Gleichheitszeichen nur noch das quadratische Glied 1x². Damit wird wie beim Schriftlichen Teilen die Klammer (x-1) multipliziert und das entstehende Zwischenergebnis x³-x² von der Ursprungsaufgabe abgezogen. Mit dem Rest wird genauso verfahren:
(x³ +5x² +2x -8)÷(x-1)= x² +6x +8
-(x³ - x²)
0x³ +6x² +2x -8
- (6x² -6x)
8x -8
- (8x -8)
0
Die Division ging glatt auf (das muss sie, wenn wir eine Nullstelle herausteilen). Für die anderen beiden Lösungen ist jetzt nur noch die Quadratische Gleichung
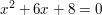
z.B. durch Quadratische Ergänzung zu lösen.
Ein mögliches Verständnisproblem beim "Herausdividieren einer Nullstelle" besteht darin, dass man vermeintlich durch 0 dividiert. Dies ist jedoch nicht der Fall, da man nicht Zahlen dividiert, sondern Polynome. Da das Polynom x-1 nicht das Nullpolynom ist, kann man (mit Rest) durch dieses Polynom dividieren.
Tipp: Horner-Schema
Das oben gezeigte ausführliche Divisionsverfahren kann man sich sehr erleichtern durch die Nutzung des Hornerschemas.
![Link auf "http://www.arndt-bruenner.de/mathe/scripts/polynomdivisionueben.htm" [link]](/images/popup.gif) http://www.arndt-bruenner.de/mathe/scripts/polynomdivisionueben.htm http://www.arndt-bruenner.de/mathe/scripts/polynomdivisionueben.htm
![Link auf "http://www.brinkmann-du.de/mathe/gost/polynomdivision_01.htm" [link]](/images/popup.gif) http://www.brinkmann-du.de/mathe/gost/polynomdivision_01.htm http://www.brinkmann-du.de/mathe/gost/polynomdivision_01.htm
![Link auf "http://de.wikipedia.org/wiki/Polynomdivision" [link]](/images/popup.gif) http://de.wikipedia.org/wiki/Polynomdivision http://de.wikipedia.org/wiki/Polynomdivision
![Link auf "http://www.arndt-bruenner.de/mathe/scripts/polynomdivision.htm" [link]](/images/popup.gif) http://www.arndt-bruenner.de/mathe/scripts/polynomdivision.htm http://www.arndt-bruenner.de/mathe/scripts/polynomdivision.htm
|