Moivre-FormelMoivre-Formel
Sowohl hohe Potenzen 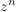 als auch Wurzeln als auch Wurzeln ![$ \wurzel[n]{z} $ $ \wurzel[n]{z} $](/teximg/2/5/00168852.png) von komplexen Zahlen von komplexen Zahlen 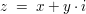 (mit (mit 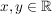 ) können mit Hilfe der "Moivre-Formel" berechnet werden. ) können mit Hilfe der "Moivre-Formel" berechnet werden.
Dabei gilt hier für 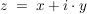 : :
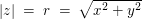 sowie sowie 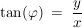
Für den Winkel 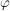 ist auch noch der jeweilige Quadrant in der Gauß'schen Zahlenebene zu berücksichtigen (siehe dazu auch: komplexe Zahlen) ist auch noch der jeweilige Quadrant in der Gauß'schen Zahlenebene zu berücksichtigen (siehe dazu auch: komplexe Zahlen)
Beispiele
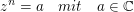
Beipiel 1
Berechnung aller Lösungen von 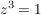
Zuerst brauchen wir für die Zahl 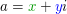 eine Darstellung der Form eine Darstellung der Form 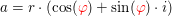
 ist der Betrag der komplexen Zahl a und errechnet sich durch ist der Betrag der komplexen Zahl a und errechnet sich durch 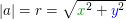
Unsere Zahl 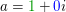 hat also den Betrag hat also den Betrag 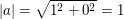
Der Winkel 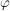 berechnet sich aus berechnet sich aus 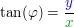 (Anm: wobei hier immer darauf geachtet werden muss, in welchem Quadranten unsere komplexe Zahl zu finden ist - d.h. er muss ggf. mit dem Wert (Anm: wobei hier immer darauf geachtet werden muss, in welchem Quadranten unsere komplexe Zahl zu finden ist - d.h. er muss ggf. mit dem Wert 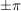 ergänzt werden). ergänzt werden).
Hier ist 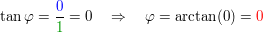
Damit habe wir schon alles, was wir für die Moivre-Formel benötigen
![$ \wurzel[n]{z} \ = \ \wurzel[n]{r}\cdot{}\left[\cos\left(\bruch{\varphi+k\cdot{}2\pi}{n}\right)+\sin\left(\bruch{\varphi+k\cdot{}2\pi}{n}\right)\cdot{}i\right]\quad \text{mit}\quad k \ = \ 0 \ ... \ (n-1) $ $ \wurzel[n]{z} \ = \ \wurzel[n]{r}\cdot{}\left[\cos\left(\bruch{\varphi+k\cdot{}2\pi}{n}\right)+\sin\left(\bruch{\varphi+k\cdot{}2\pi}{n}\right)\cdot{}i\right]\quad \text{mit}\quad k \ = \ 0 \ ... \ (n-1) $](/teximg/9/3/02347439.png)
Rechnungen:
![$ z_1=\wurzel[3]{1}\cdot{}\left[\underbrace{\cos\left(\bruch{\red{0}+0\cdot{}2\pi}{3}\right)}_{=1}+\underbrace{\sin\left(\bruch{\red{0}+0\cdot{}2\pi}{3}\right)}_{=0}\cdot{}i\right]=1 $ $ z_1=\wurzel[3]{1}\cdot{}\left[\underbrace{\cos\left(\bruch{\red{0}+0\cdot{}2\pi}{3}\right)}_{=1}+\underbrace{\sin\left(\bruch{\red{0}+0\cdot{}2\pi}{3}\right)}_{=0}\cdot{}i\right]=1 $](/teximg/8/3/02347438.png)
![$ z_2=\wurzel[3]{1}\cdot{}\left[\underbrace{\cos\left(\bruch{\red{0}+1\cdot{}2\pi}{3}\right)}_{=-\bruch{1}{2}}+\underbrace{\sin\left(\bruch{\red{0}+1\cdot{}2\pi}{3}\right)}_{=\bruch{\wurzel{3}}{2}}\cdot{}i\right]=-\bruch{1}{2}+\bruch{\wurzel{3}}{2}\cdot{}i $ $ z_2=\wurzel[3]{1}\cdot{}\left[\underbrace{\cos\left(\bruch{\red{0}+1\cdot{}2\pi}{3}\right)}_{=-\bruch{1}{2}}+\underbrace{\sin\left(\bruch{\red{0}+1\cdot{}2\pi}{3}\right)}_{=\bruch{\wurzel{3}}{2}}\cdot{}i\right]=-\bruch{1}{2}+\bruch{\wurzel{3}}{2}\cdot{}i $](/teximg/0/4/02347440.png)
![$ z_3=\wurzel[3]{1}\cdot{}\left[\underbrace{\cos\left(\bruch{\red{0}+2\cdot{}2\pi}{3}\right)}_{=-\bruch{1}{2}}+\underbrace{\sin\left(\bruch{\red{0}+2\cdot{}2\pi}{3}\right)}_{=-\bruch{\wurzel{3}}{2}}\cdot{}i\right]=-\bruch{1}{2}-\bruch{\wurzel{3}}{2}\cdot{}i $ $ z_3=\wurzel[3]{1}\cdot{}\left[\underbrace{\cos\left(\bruch{\red{0}+2\cdot{}2\pi}{3}\right)}_{=-\bruch{1}{2}}+\underbrace{\sin\left(\bruch{\red{0}+2\cdot{}2\pi}{3}\right)}_{=-\bruch{\wurzel{3}}{2}}\cdot{}i\right]=-\bruch{1}{2}-\bruch{\wurzel{3}}{2}\cdot{}i $](/teximg/1/4/02347441.png)
Beispiel 2
Berechnung aller Lösungen von 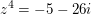
Zuerst brauchen wir für die Zahl 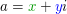 eine Darstellung der Form eine Darstellung der Form 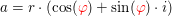
 ist der Betrag der komplexen Zahl a und errechnet sich durch ist der Betrag der komplexen Zahl a und errechnet sich durch 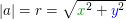
Unsere Zahl 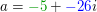 hat also den Betrag hat also den Betrag 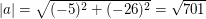
Der Winkel 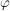 berechnet sich aus berechnet sich aus 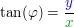 (Anm: wobei hier immer darauf geachtet werden muss, in welchem Quadranten unsere komplexe Zahl zu finden ist - d.h. er muss ggf. mit dem Wert (Anm: wobei hier immer darauf geachtet werden muss, in welchem Quadranten unsere komplexe Zahl zu finden ist - d.h. er muss ggf. mit dem Wert 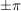 ergänzt werden). Wir befinden uns im 3. Quadranten und benötigen daher die Erweiterung mit ergänzt werden). Wir befinden uns im 3. Quadranten und benötigen daher die Erweiterung mit  , um auf den Hauptwert zu kommen. , um auf den Hauptwert zu kommen.
Hier ist 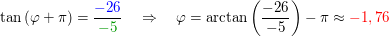
Damit habe wir schon alles, was wir für die Moivre-Formel benötigen
![$ \wurzel[n]{z} \ = \ \wurzel[n]{r}\cdot{}\left[\cos\left(\bruch{\varphi+k\cdot{}2\pi}{n}\right)+\sin\left(\bruch{\varphi+k\cdot{}2\pi}{n}\right)\cdot{}i\right]\quad \text{mit}\quad k \ = \ 0 \ ... \ (n-1) $ $ \wurzel[n]{z} \ = \ \wurzel[n]{r}\cdot{}\left[\cos\left(\bruch{\varphi+k\cdot{}2\pi}{n}\right)+\sin\left(\bruch{\varphi+k\cdot{}2\pi}{n}\right)\cdot{}i\right]\quad \text{mit}\quad k \ = \ 0 \ ... \ (n-1) $](/teximg/9/3/02347439.png)
Rechnungen:
Mit ![$ \sqrt[4]{\sqrt{k}}=\sqrt[8]{k} $ $ \sqrt[4]{\sqrt{k}}=\sqrt[8]{k} $](/teximg/9/9/02347399.png) folgen u.a. Lösungen folgen u.a. Lösungen
![$ z_1\approx\wurzel[8]{701}\cdot{}\left[\cos\left(\bruch{\red{-1,76}+0\cdot{}2\pi}{4}\right)}+\sin\left(\bruch{\red{-1,76}+0\cdot{}2\pi}{4}\right)}\cdot{}i\right]\approx 2,052-0,966\cdot{}i $ $ z_1\approx\wurzel[8]{701}\cdot{}\left[\cos\left(\bruch{\red{-1,76}+0\cdot{}2\pi}{4}\right)}+\sin\left(\bruch{\red{-1,76}+0\cdot{}2\pi}{4}\right)}\cdot{}i\right]\approx 2,052-0,966\cdot{}i $](/teximg/2/4/02347442.png)
![$ z_2\approx\wurzel[8]{701}\cdot{}\left[\cos\left(\bruch{\red{-1,76}+1\cdot{}2\pi}{4}\right)}+\sin\left(\bruch{\red{-1,76}+1\cdot{}2\pi}{4}\right)}\cdot{}i\right]\approx 0,966+2,052\cdot{}i $ $ z_2\approx\wurzel[8]{701}\cdot{}\left[\cos\left(\bruch{\red{-1,76}+1\cdot{}2\pi}{4}\right)}+\sin\left(\bruch{\red{-1,76}+1\cdot{}2\pi}{4}\right)}\cdot{}i\right]\approx 0,966+2,052\cdot{}i $](/teximg/3/4/02347443.png)
![$ z_3\approx\wurzel[8]{701}\cdot{}\left[\cos\left(\bruch{\red{-1,76}+2\cdot{}2\pi}{4}\right)}+\sin\left(\bruch{\red{-1,76}+2\cdot{}2\pi}{4}\right)}\cdot{}i\right]\approx -2,052+0,966\cdot{}i $ $ z_3\approx\wurzel[8]{701}\cdot{}\left[\cos\left(\bruch{\red{-1,76}+2\cdot{}2\pi}{4}\right)}+\sin\left(\bruch{\red{-1,76}+2\cdot{}2\pi}{4}\right)}\cdot{}i\right]\approx -2,052+0,966\cdot{}i $](/teximg/0/5/02347450.png)
![$ z_4\approx\wurzel[8]{701}\cdot{}\left[\cos\left(\bruch{\red{-1,76}+3\cdot{}2\pi}{4}\right)}+\sin\left(\bruch{\red{-1,76}+3\cdot{}2\pi}{4}\right)}\cdot{}i\right]\approx -0,966-2,052\cdot{}i $ $ z_4\approx\wurzel[8]{701}\cdot{}\left[\cos\left(\bruch{\red{-1,76}+3\cdot{}2\pi}{4}\right)}+\sin\left(\bruch{\red{-1,76}+3\cdot{}2\pi}{4}\right)}\cdot{}i\right]\approx -0,966-2,052\cdot{}i $](/teximg/2/5/02347452.png)
|