Benutzer:tobit09/Beweis-Tutorial A10Beweis-Tutorial
 3. "es existiert"-Aussagen 3. "es existiert"-Aussagen
Lösungsvorschlag Aufgabe 10
Aufgabe:
Seien 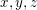 natürliche Zahlen. Gelte natürliche Zahlen. Gelte 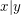 und und 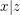 . Zeige . Zeige 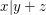 . .
Überlegungen zur Lösung:
Gegeben:
Natürliche Zahlen 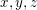 . .
x|y, d.h. es existiert eine natürliche Zahl 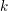 mit mit 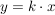 . .
x|z, d.h. es existiert eine natürliche Zahl 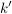 mit mit 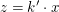 . .
Zu zeigen:
x|y+z, d.h. es existiert eine natürliche Zahl 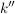 mit mit 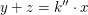 . .
Beispielsweise mit Schmierzettel-Methode ein Beispiel für 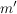 finden: finden:
1. Eine geeignete natürliche Zahl 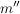 muss muss
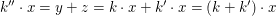
erfüllen. Falls 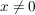 gilt (was im Falle, dass man gilt (was im Falle, dass man 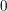 nicht zu den natürlichen Zahlen zählt, sowieso erfüllt ist), folgt nicht zu den natürlichen Zahlen zählt, sowieso erfüllt ist), folgt 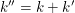 . .
2. Die Zahl 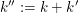 ist tatsächlich eine natürliche Zahl (da ist tatsächlich eine natürliche Zahl (da 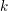 und und 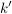 natürliche Zahlen sind) und erfüllt natürliche Zahlen sind) und erfüllt
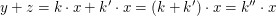
(auch im Falle x=0).
Lösungsvorschlag:
Da 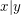 gilt, existiert eine natürliche Zahl gilt, existiert eine natürliche Zahl 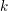 mit mit 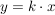 . .
Da 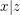 gilt, existiert eine natürliche Zahl gilt, existiert eine natürliche Zahl 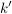 mit mit 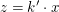 . .
Da 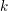 und und 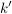 natürliche Zahlen sind, ist auch natürliche Zahlen sind, ist auch 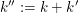 eine natürliche Zahl. Sie erfüllt eine natürliche Zahl. Sie erfüllt
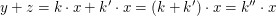 . .
Also gilt 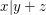 . .
|