Benutzer:tobit09/Beweis-Tutorial existiertBeweis-Tutorial
 1. Vorbereitungen: Definitionen 1. Vorbereitungen: Definitionen  Inhaltsverzeichnis Inhaltsverzeichnis  3. "für alle"-Aussagen 3. "für alle"-Aussagen
2. "es existiert"-Aussagen
Wie zeige ich eine "es existiert"-Aussage?
Beispiel Die natürliche Zahl 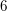 ist gerade. ist gerade.
Das wollen wir nun beweisen. Nach den Übungsaufgaben aus 2. Vorbereitungen: Definitionen ist der erste Schritt dazu hoffentlich kein Problem mehr: Notieren, was die Behauptung eigentlich bedeutet. Nämlich:
Es existiert eine natürliche Zahl  mit mit 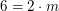 . .
Zu zeigen ist also diese "es-existiert"-Aussage. Wie kann man so eine "es existiert"-Aussage beweisen? Man nennt hier einfach eine konkrete natürliche Zahl  , die wie gewünscht , die wie gewünscht 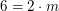 erfüllt: Die Zahl erfüllt: Die Zahl 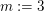 (das Zeichen (das Zeichen 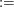 bedeutet hier: bedeutet hier:  wird definiert durch wird definiert durch 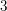 ) leistet das Gewünschte, denn ) leistet das Gewünschte, denn 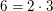 . Damit ist auch schon gezeigt, dass eine natürliche Zahl . Damit ist auch schon gezeigt, dass eine natürliche Zahl  mit mit 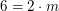 existiert: Wir haben ja eine solche Zahl existiert: Wir haben ja eine solche Zahl  gefunden. gefunden.
Unseren Beweis können wir nun z.B. wie folgt notieren:
Die natürliche Zahl 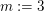 erfüllt erfüllt 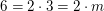 . Insbesondere existiert eine natürliche Zahl . Insbesondere existiert eine natürliche Zahl  mit mit 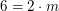 . Also ist 6 gerade. . Also ist 6 gerade.
Das ist eigentlich schon alles, was es zum Beweis von "es existiert"-Aussagen zu sagen gibt: Man gibt ein konkretes Beispiel (oben: die Zahl 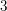 ) an und weist nach, dass es das Gewünschte leistet. ) an und weist nach, dass es das Gewünschte leistet.
Wie finde ich so ein Beispiel?
Das fragt sich vielleicht manch einer insbesondere bei schwierigeren Aufgaben. Wie komme ich beispielsweise oben darauf, dass mir gerade die Zahl 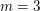 weiterhilft? Eine pauschale Antwort auf solche Fragen gibt es nicht! Je schwieriger die Probleme werden, desto mehr ist die "Genialität" des Mathematikers/der Mathematikerin gefordert, ein solches Beispiel zu finden. Manchmal hilft beispielsweise "wildes Rumprobieren", manchmal eine gute Anschauung (z.B. von Funktionen anhand ihres Graphen) oder Vorstellung bei der Suche. weiterhilft? Eine pauschale Antwort auf solche Fragen gibt es nicht! Je schwieriger die Probleme werden, desto mehr ist die "Genialität" des Mathematikers/der Mathematikerin gefordert, ein solches Beispiel zu finden. Manchmal hilft beispielsweise "wildes Rumprobieren", manchmal eine gute Anschauung (z.B. von Funktionen anhand ihres Graphen) oder Vorstellung bei der Suche.
Eine Such-Methode, die ich "Schmierzettel-Methode" nenne, möchte ich jedoch an obigem Beispiel vorstellen: Man fragt sich: Wie müsste eine natürliche Zahl  aussehen, wenn sie wie gewünscht aussehen, wenn sie wie gewünscht 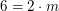 erfüllen würde? Man tut also (auf einem Schmierzettel) so, als hätte man schon ein Beispiel, und versucht, Informationen über das Beispiel zu gewinnen. Aus erfüllen würde? Man tut also (auf einem Schmierzettel) so, als hätte man schon ein Beispiel, und versucht, Informationen über das Beispiel zu gewinnen. Aus 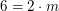 folgt durch dividieren durch 2 auf beiden Seiten der Gleichung sofort folgt durch dividieren durch 2 auf beiden Seiten der Gleichung sofort 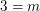 . Was sagt uns das? Wenn wir überhaupt eine Chance haben sollten, eine Zahl . Was sagt uns das? Wenn wir überhaupt eine Chance haben sollten, eine Zahl  mit mit 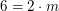 zu finden, muss diese Zahl zu finden, muss diese Zahl 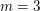 lauten. Wir haben mit dieser Schmierzettel-Überlegung noch nicht etwa gezeigt, dass lauten. Wir haben mit dieser Schmierzettel-Überlegung noch nicht etwa gezeigt, dass 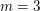 wirklich ein Beispiel für eine Zahl wirklich ein Beispiel für eine Zahl  mit mit 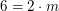 ist! Ob ist! Ob 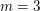 nun die einzige mögliche Wahl für ein Beispiel ist (wie unsere Schmierzettel-Überlegung zeigt), ist für den fertigen Beweis irrelevant. Diese Überlegung hat uns nur geholfen, ein Beispiel überhaupt zu finden. Im fertigen Beweis müssen wir uns nicht dafür rechtfertigen, wie wir auf das Beispiel gekommen sind. Wir können also, nachdem wir auf nun die einzige mögliche Wahl für ein Beispiel ist (wie unsere Schmierzettel-Überlegung zeigt), ist für den fertigen Beweis irrelevant. Diese Überlegung hat uns nur geholfen, ein Beispiel überhaupt zu finden. Im fertigen Beweis müssen wir uns nicht dafür rechtfertigen, wie wir auf das Beispiel gekommen sind. Wir können also, nachdem wir auf 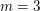 gekommen sind, getrost den Schmierzettel wegwerfen. Für den fertigen Beweis interessiert nur, dass gekommen sind, getrost den Schmierzettel wegwerfen. Für den fertigen Beweis interessiert nur, dass 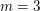 das Gewünschte leistet. das Gewünschte leistet.
Zusammengefasst lautet die "Schmierzettel-Methode" also:
1. Nimm auf einem Schmierzettel an, du hättest schon ein Beispiel, das das Gewünschte leistet. Ziehe Schlussfolgerungen daraus, um Informationen zu gewinnen, welche Eigenschaften das Beispiel dann notwendigerweise haben müsste.
2. Gib ein Beispiel mit diesen Eigenschaften an und zeige (unabhängig von den Schmierzettel-Überlegungen!), dass dieses Beispiel das Gewünschte leistet.
Aufgabe 5 Zeige, dass 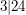 gilt. Lösungsvorschlag gilt. Lösungsvorschlag
Aufgabe 6 Zeige, dass eine reelle Zahl  existiert mit existiert mit 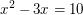 . Lösungsvorschlag . Lösungsvorschlag
Aufgabe 7 Seien 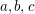 reelle Zahlen mit reelle Zahlen mit 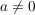 . Zeige, dass eine reelle Zahl . Zeige, dass eine reelle Zahl  existiert mit existiert mit 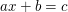 . Lösungsvorschlag . Lösungsvorschlag
Aufgabe 8 Sei  eine reelle Zahl. Zeige, dass es eine reelle Zahl eine reelle Zahl. Zeige, dass es eine reelle Zahl 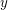 mit mit 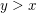 gibt. Lösungsvorschlag gibt. Lösungsvorschlag
Wie benutze ich eine "es existiert"-Aussage?
Beispiel Seien  und und 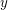 gerade natürliche Zahlen. Dann ist auch die natürliche Zahl gerade natürliche Zahlen. Dann ist auch die natürliche Zahl 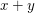 gerade. gerade.
Fangen wir wieder mit unseren Routine-Vorbereitungen an und überlegen uns, was die Voraussetzungen und die Behauptung jeweils bedeuten:
Gegeben:
Natürliche Zahlen  und und 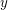 . .
 gerade, d.h. es existiert eine natürliche Zahl gerade, d.h. es existiert eine natürliche Zahl  mit mit 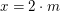 . .
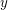 gerade, d.h. es existiert eine natürliche Zahl gerade, d.h. es existiert eine natürliche Zahl 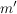 mit mit 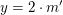 . .
Zu zeigen:
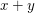 gerade, d.h. es existiert eine natürliche Zahl gerade, d.h. es existiert eine natürliche Zahl 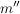 mit mit 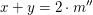 . .
Wir müssen also wieder eine "es existiert"-Aussage beweisen. Wie das geht, wissen wir schon: Wir müssen ein Beispiel für eine Zahl 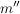 mit mit 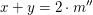 finden. Das Neue ist nun, dass wir irgendwie die durch die Voraussetzungen gegebenen "es existiert"-Aussagen ins Spiel bringen müssen. Das geht für die Voraussetzung " finden. Das Neue ist nun, dass wir irgendwie die durch die Voraussetzungen gegebenen "es existiert"-Aussagen ins Spiel bringen müssen. Das geht für die Voraussetzung " gerade" wie folgt: gerade" wie folgt:
"Es existiert eine natürliche Zahl  mit mit 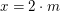 . Wir wählen eine solche Zahl . Wir wählen eine solche Zahl  (das können wir tun, denn es gibt ja eine solche Zahl)." (das können wir tun, denn es gibt ja eine solche Zahl)."
Ab jetzt können wir annehmen, dass wir eine natürliche Zahl  mit mit 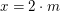 haben. Genauso verfahren wir mit der Voraussetzung " haben. Genauso verfahren wir mit der Voraussetzung "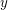 gerade": gerade":
"Es existiert eine natürliche Zahl 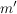 mit mit 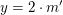 . Wir wählen eine solche Zahl . Wir wählen eine solche Zahl 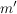 (das können wir tun, denn es gibt ja eine solche Zahl)." (das können wir tun, denn es gibt ja eine solche Zahl)."
Wir haben also nun natürliche Zahlen m und 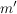 mit mit 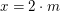 und und 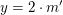 (*). Wir suchen wie gesagt eine natürliche Zahl (*). Wir suchen wie gesagt eine natürliche Zahl 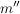 mit mit 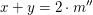 . .
Zum Beispiel mit der Schmierzettel-Methode:
1. Wenn eine Zahl natürliche Zahl 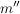 der Gleichung der Gleichung 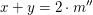 genügen soll, muss (Einsetzen der Gleichungen (*)) notwendigerweise genügen soll, muss (Einsetzen der Gleichungen (*)) notwendigerweise
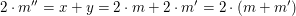
gelten, also 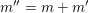 . .
2. Weisen wir nach, dass 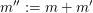 das Gewünschte leistet, also eine natürliche Zahl ist, die das Gewünschte leistet, also eine natürliche Zahl ist, die 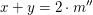 erfüllt: Da m und erfüllt: Da m und 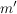 natürliche Zahlen sind, ist auch natürliche Zahlen sind, ist auch 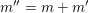 eine natürliche Zahl. Sie erfüllt eine natürliche Zahl. Sie erfüllt
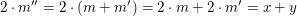
wie gewünscht.
Damit haben wir unseren Beweis gefunden! Schreiben wir ihn noch ordentlich im Zusammenhang auf:
Da  gerade ist, existiert eine natürliche Zahl gerade ist, existiert eine natürliche Zahl  mit mit 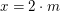 . .
Wir wählen eine solche Zahl  (das können wir tun, denn es gibt ja eine solche Zahl). (das können wir tun, denn es gibt ja eine solche Zahl).
Da 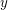 gerade ist, existiert eine natürliche Zahl gerade ist, existiert eine natürliche Zahl 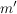 mit mit 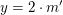 . .
Wir wählen eine solche Zahl 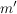 (das können wir tun, denn es gibt ja eine solche Zahl). (das können wir tun, denn es gibt ja eine solche Zahl).
Da  und und 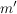 natürliche Zahlen sind, ist auch natürliche Zahlen sind, ist auch 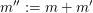 eine natürliche Zahl. Sie erfüllt eine natürliche Zahl. Sie erfüllt
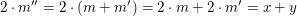 . .
Insbesondere existiert eine natürliche Zahl 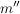 mit mit 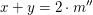 . .
Also ist 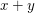 gerade. gerade.
Es ist üblich, die kursiv gedruckten Zeilen wegzulassen. So gut wie immer, wenn innerhalb eines Beweises etwas steht wie "es existiert eine natürliche Zahl  mit...", ist automatisch gemeint, dass wir eine solche Zahl mit...", ist automatisch gemeint, dass wir eine solche Zahl  wählen. Diese Konvention erspart einem viel Schreibarbeit... wählen. Diese Konvention erspart einem viel Schreibarbeit...
Aufgabe 9 Sei  eine gerade natürliche Zahl. Zeige, dass dann auch die natürliche Zahl eine gerade natürliche Zahl. Zeige, dass dann auch die natürliche Zahl  gerade ist. Lösungsvorschlag gerade ist. Lösungsvorschlag
Aufgabe 10 Seien 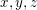 natürliche Zahlen. Gelte natürliche Zahlen. Gelte 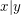 und und 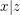 . Zeige . Zeige 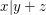 . Lösungsvorschlag . Lösungsvorschlag
Aufgabe 11 Seien 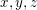 natürliche Zahlen. Gelte natürliche Zahlen. Gelte 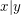 . Zeige . Zeige 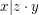 . Lösungsvorschlag . Lösungsvorschlag
Aufgabe 12 Seien 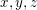 natürliche Zahlen. Gelte natürliche Zahlen. Gelte 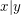 und und 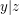 . Zeige . Zeige 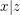 . Lösungsvorschlag . Lösungsvorschlag
Aufgabe 13 Seien  und und 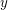 natürliche Zahlen mit natürliche Zahlen mit 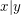 . Sei . Sei  eine weitere natürliche Zahl. Zeige eine weitere natürliche Zahl. Zeige 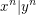 . Lösungsvorschlag . Lösungsvorschlag
|