Erzeugendensystem einer GruppeDefinition Erzeugendensystem einer Gruppe
Universität
Gegeben sei eine Gruppe G und eine Teilmenge 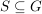 . Will man Aussagen über S machen, die durch die Gruppeneigenschaften bedingt sind, so ist es zweckmäßig, alle Elemente von G außer acht zu lassen, die mit S nichts zu tun haben. Dies geschieht so, dass man die kleinste Untergruppe von G aufsucht, die S enthält. Daß es eine solche Untergruppe gibt, folgt aus der Tatsache, dass der beliebige Durchschnitt von Untergruppen wieder eine Untergruppe ist: . Will man Aussagen über S machen, die durch die Gruppeneigenschaften bedingt sind, so ist es zweckmäßig, alle Elemente von G außer acht zu lassen, die mit S nichts zu tun haben. Dies geschieht so, dass man die kleinste Untergruppe von G aufsucht, die S enthält. Daß es eine solche Untergruppe gibt, folgt aus der Tatsache, dass der beliebige Durchschnitt von Untergruppen wieder eine Untergruppe ist:
Es sei G eine Gruppe und 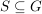 . Die Gruppe . Die Gruppe
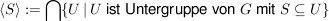
heißt die von S erzeugte Untergruppe von G. Ist 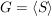 , dann heißt G von S erzeugt und S ein Erzeugendensystem von G. , dann heißt G von S erzeugt und S ein Erzeugendensystem von G.
G heißt endlich erzeugt, wenn es ein endliches Erzeugendensystem 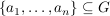 gibt. In diesem Fall schreiben wir gibt. In diesem Fall schreiben wir 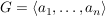 . .
Es ist 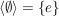 , ,  . Jede endliche Gruppe ist natürlich auch endlich erzeugt. . Jede endliche Gruppe ist natürlich auch endlich erzeugt.
Folgende Eigenschaften ersieht man sofort aus der Definition von 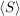 : :
a) 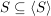
b)  für jede Untergruppe U, die S enthält, für jede Untergruppe U, die S enthält,
denn der Durchschnitt über alle solche Untergruppen ist natürlich in U enthalten.
In dem Sinne von a) und b) sagen wir, dass 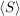 die kleinste Untergruppe von G ist, die S enthält. Ist S bereits eine Untergruppe, dann gilt b) auch für U=S, d.h. die kleinste Untergruppe von G ist, die S enthält. Ist S bereits eine Untergruppe, dann gilt b) auch für U=S, d.h. 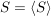 . .
Aus der Definition von 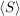 kann man einige Eigenschaften von kann man einige Eigenschaften von 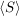 leicht ableiten, sie ist allerdings zur praktischen Bestimmung der von einer Menge erzeugten Untergruppe nicht gut geeignet. Es ist recht mühsam, alle Untergruppe aufzusuchen, die S enthalten. Aber einfache Überlegungen helfen da weiter. Jede Untergruppe, die S enthält, muss auch SS und leicht ableiten, sie ist allerdings zur praktischen Bestimmung der von einer Menge erzeugten Untergruppe nicht gut geeignet. Es ist recht mühsam, alle Untergruppe aufzusuchen, die S enthalten. Aber einfache Überlegungen helfen da weiter. Jede Untergruppe, die S enthält, muss auch SS und 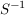 und damit alle endlichen Produkte enthalten, die man aus Elementen aus und damit alle endlichen Produkte enthalten, die man aus Elementen aus 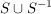 bilden kann. Betrachten wir daher die Menge bilden kann. Betrachten wir daher die Menge
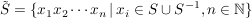 . .
Nach dem soeben gesagten gilt: 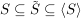 . .
Nun ist mit 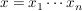 , , 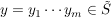 auch auch 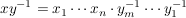 ein endliches Produkt von Elementen aus ein endliches Produkt von Elementen aus 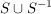 , also , also 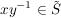 . Damit ist . Damit ist  eine Untergruppe, die S enthält. Die obige Eigenschaft b) zeigt: eine Untergruppe, die S enthält. Die obige Eigenschaft b) zeigt: 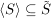 und mit der vorher gezeigten Inklusion und mit der vorher gezeigten Inklusion  folgt: folgt: 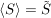 . Wir haben bewiesen: . Wir haben bewiesen:
Ist G eine Gruppe und S eine nichtleere Teilmenge von G, dann besteht 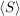 , die von S erzeugte Untergruppe, aus allen endlichen Produkten von Elementen aus , die von S erzeugte Untergruppe, aus allen endlichen Produkten von Elementen aus 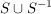 . .
Dieser Satz erlaubt nicht nur eine Berechnung von 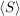 , sondern zeigt auch, dass Homomorphismen bereits durch die Werte auf einem Erzeugendensystem eindeutig bestimmt sind: , sondern zeigt auch, dass Homomorphismen bereits durch die Werte auf einem Erzeugendensystem eindeutig bestimmt sind:
Ist 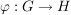 ein Gruppenhomomorphismus und ein Gruppenhomomorphismus und 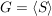 , dann ist , dann ist 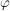 bereits durch die Bilder der Elemente aus S eindeutig bestimmt. Äquivalent dazu: Sind bereits durch die Bilder der Elemente aus S eindeutig bestimmt. Äquivalent dazu: Sind 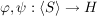 Homomorphismen mit Homomorphismen mit 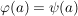 für alle für alle 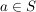 , dann ist , dann ist 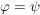 . .
Die genaue Bestimmung der Struktur der von einer Menge 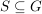 erzeugten Untergruppe von G ist im allgemeinen eine höchst komplizierte Angelegenheit; auch dann noch, wenn S nur zwei Elemente enthält. Der einfachste Fall, erzeugten Untergruppe von G ist im allgemeinen eine höchst komplizierte Angelegenheit; auch dann noch, wenn S nur zwei Elemente enthält. Der einfachste Fall, 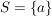 , lässt sich einfach und in allen Details übersehen, siehe hier: zyklisch. , lässt sich einfach und in allen Details übersehen, siehe hier: zyklisch.
Quelle: isbn3446130799
|