HäufungspunktDefinition Häufungspunkt (einer Folge)
Universität
Sei  eine Folge reeller (bzw. komplexer) Zahlen. eine Folge reeller (bzw. komplexer) Zahlen.
Ein Punkt 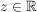 (bzw. (bzw. 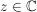 ) heißt Häufungspunkt (der Folge ) heißt Häufungspunkt (der Folge  ), wenn in jeder Umgebung von z unendlich viele Folgenglieder von ), wenn in jeder Umgebung von z unendlich viele Folgenglieder von  liegen. liegen.
Wichtige Sätze
Satz Sei  eine Folge reeller (bzw. komplexer) Zahlen und 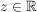 (bzw. 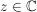 .
z Häufungspunkt von    besitzt eine gegen z konvergente Teilfolge.
Satz von Weierstraß-Bolzano Jede beschränkte Folge reeller (bzw. komplexer) Zahlen besitzt einen Häufungspunkt.
Definition Häufungspunkt (einer Menge)
Für den Raum 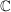 bzw. bzw. 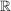
Sie A eine Teilmenge von  ( (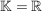 oder oder 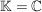 ). ).
Ein Punkt 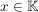 heißt Häufungspunkt von A, wenn in jeder Umgebung von x unendliche viele Elemente von A liegen. heißt Häufungspunkt von A, wenn in jeder Umgebung von x unendliche viele Elemente von A liegen.
Für metrische Räume
Sei (M,d) metrischer Raum, 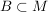 . .
 heißt Häufungspunkt von B, wenn es in jeder Umgebung von x Punkte aus B gibt, die von x verschieden sind. heißt Häufungspunkt von B, wenn es in jeder Umgebung von x Punkte aus B gibt, die von x verschieden sind.
Für topologische Räume
Seien X ein topologischer Raum und 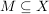 . .
Ein Punkt 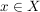 heißt ein Häufungspunkt von M, wenn in jeder Umgebung von x ein von x verschiedener Punkt aus M liegt. heißt ein Häufungspunkt von M, wenn in jeder Umgebung von x ein von x verschiedener Punkt aus M liegt.
Wichtige Sätze
|