ScheitelpunktformDie Scheitelpunktform einer Parabel kann man so schreiben:
Dabei liest man ab:
Der Scheitelpunkt liegt bei 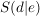 . .
Erklärung:
Die Normalparabel 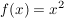 mit Scheitelpunkt mit Scheitelpunkt 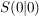
wird
- um
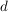 nach rechts verschoben, falls nach rechts verschoben, falls 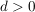 oder um oder um 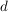 nach links verschoben, falls nach links verschoben, falls 
- mit Faktor
 gestreckt/gestaucht gestreckt/gestaucht
- und um
 nach oben nach oben 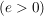 bzw. nach unten bzw. nach unten  verschoben. verschoben.
Beispielrechnung:
Nehmen wir mal zum Beispiel die Parabel  und formen diese in die Scheitelpunktsform um: und formen diese in die Scheitelpunktsform um:

Zunächst den Zahlenwert vor dem  ausklammern: ausklammern:
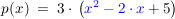
Nun überlegen wir uns, wie wir den Term 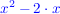 zu einer binomischen Formel ergänzen können. Dafür nehmen wir uns den Term vor dem zu einer binomischen Formel ergänzen können. Dafür nehmen wir uns den Term vor dem  , halbieren ihn und quadrieren diesen Wert: , halbieren ihn und quadrieren diesen Wert:

Diesen Wert addieren wir nun und ziehen ihn gleich wieder ab, damit wir die Funktionsvorschrift nicht verändern:
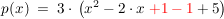
Nun können wir  zusammenfassen mittels binomischer Formel zu: zusammenfassen mittels binomischer Formel zu: 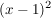 : :
![$ p(x) \ = \ 3\cdot{}\left[(x-1)^2-1+5\right] $ $ p(x) \ = \ 3\cdot{}\left[(x-1)^2-1+5\right] $](/teximg/0/4/00740840.png)
![$ p(x) \ = \ 3\cdot{}\left[(x-1)^2+4\right] $ $ p(x) \ = \ 3\cdot{}\left[(x-1)^2+4\right] $](/teximg/1/4/00740841.png)
Nun die  wieder hineinmultiplizieren: wieder hineinmultiplizieren:
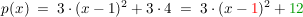
Damit können wir nun den Scheitelpunkt ablesen mit 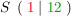 . .
|