VielfachenmengeDie Vielfachenmenge ist die Menge aller (natürlichen) Vielfachen einer Zahl, z.B.
Manche Quellen behandeln die Null ebenfalls als Vielfache (jeder Zahl), dann lautet die obige Vielfachenmenge 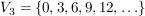 . Dies hängt wohl davon ab, ob der jeweilige Autor unter den natürlichen Zahlen die Menge . Dies hängt wohl davon ab, ob der jeweilige Autor unter den natürlichen Zahlen die Menge 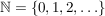 oder die Menge oder die Menge 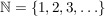 versteht. In diesem Artikel gilt: versteht. In diesem Artikel gilt: 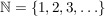
Formal läßt sich die Vielfachenmenge definieren als:
(Dies wird so gelesen: Die Vielfachenmenge der Zahl  ist die Menge aller natürlichen Zahlen, von denen ist die Menge aller natürlichen Zahlen, von denen  ein Teiler ist.) ein Teiler ist.)
Mithilfe von Vielfachenmengen läßt sich leicht das kgV zweier Zahlen (das kleinste gemeinsame Vielfache) finden:
Beispiel: 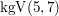
Bilde zunächst 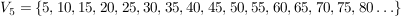 und und 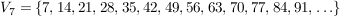 . .
Stelle dann die Schnittmenge auf: 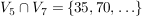 . .
Das 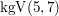 ist dann das kleinste Element dieser Schnittmenge, hier also 35. ist dann das kleinste Element dieser Schnittmenge, hier also 35.
Eigenschaften der Vielfachenmenge
- Für alle n>0 ist n in ihrer Vielfachenmenge enthalten:
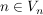 für alle n>0 für alle n>0
- Das kleinste gemeinsame Vielfache (
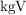 ) zweier Zahlen m und n ist das kleinste Element der Schnittmenge der beiden Vielfachenmengen: ) zweier Zahlen m und n ist das kleinste Element der Schnittmenge der beiden Vielfachenmengen: 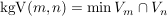
- m ist ein Teiler von n, genau dann wenn
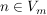
Siehe auch Teilermenge, kgV, ggT
|