FunktionentheorieSkript1 Inhaltsverzeichnis Inhaltsverzeichnis  §2 Komplex differenzierbare Funktionen §2 Komplex differenzierbare Funktionen
§1 Komplexe Zahlen und Polynome
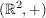 ist mit der Vektoraddition "+" eine abelsche Gruppe ist mit der Vektoraddition "+" eine abelsche Gruppe
Definiert man eine Multiplikation  für zwei Elemente für zwei Elemente 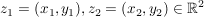 als als
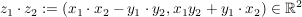
wird 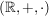 zu einem kommutativer Körper mit Einselement zu einem kommutativer Körper mit Einselement 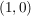 . .
Satz 1 Körper 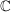 der komplexen Zahlen der komplexen Zahlen
(i) Die Zuordnung 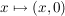 ist ein Körperhomomorphismus ist ein Körperhomomorphismus 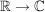
Man identifiziert  mit mit 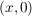 und faßt und faßt 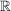 als Teilkörper von als Teilkörper von 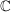 auf. auf.
(ii) Die Zuordnung 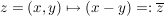 ist ein Körperautomorphismus von ist ein Körperautomorphismus von 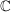 der Ordnung 2 (d.h. der Ordnung 2 (d.h. 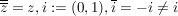 ) )
Es sei 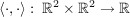 das kanonische Skalarprodukt (d.h. das kanonische Skalarprodukt (d.h. 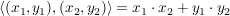 ). ).
Def 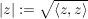 heißt Betrag von heißt Betrag von 
Es gilt: 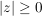 und und 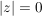  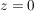
Satz 1' Für alle 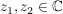 gilt: gilt:
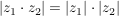
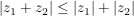 (Dreiecksungleichung) (Dreiecksungleichung)
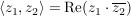 mit mit 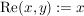
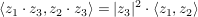
__Satz 1''C__
(i) Zu 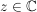 , , 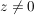 , existiert genau ein , existiert genau ein 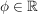 , ,  , mit , mit 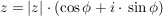
(ii) Es sei 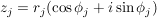 , , 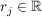 , , 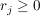
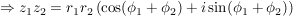
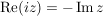
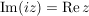
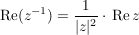
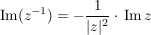
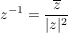
Folgerung (zu Satz 1)C__ Es sei 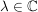 , , 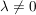 , und , und  , , 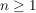
 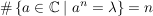 ---
---
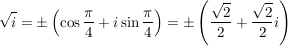 ---
Es sei
---
Es sei 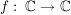 eine Zuordnung.
Def f heißt polynomial, wenn gilt: Es gibt eine Zuordnung.
Def f heißt polynomial, wenn gilt: Es gibt 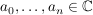 mit mit
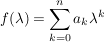 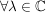 ---
Es gilt:
(i) Es sei
---
Es gilt:
(i) Es sei 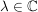 , , 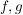 polynomiale Abbildungen polynomiale Abbildungen 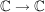  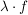 und und 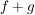 sind polynomiale Abbildungen.
(ii) sind polynomiale Abbildungen.
(ii) ![$ \IC[z] $ $ \IC[z] $](/teximg/2/0/00388902.png) :=Gesamtheit der komplexen Polynome (=polynomialen Abbildungen) :=Gesamtheit der komplexen Polynome (=polynomialen Abbildungen) ![$ (\IC[z],+,\cdot{}) $ $ (\IC[z],+,\cdot{}) $](/teximg/3/0/00388903.png) ist ist 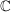 -Vektorraum
(iii) -Vektorraum
(iii) 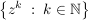 ist ist 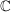 -Vektorraumbasis von -Vektorraumbasis von ![$ \IC[z] $ $ \IC[z] $](/teximg/2/0/00388902.png) ---
Def Man nennt n den Grad von f (in Zeichen:
---
Def Man nennt n den Grad von f (in Zeichen: 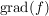 ) und ) und 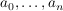 die Koeffizienten von f.
---
Es gilt:
(i) Sind die Koeffizienten von f.
---
Es gilt:
(i) Sind ![$ f,g\in\IC[z] $ $ f,g\in\IC[z] $](/teximg/7/0/00388907.png) , so ist , so ist ![$ f\cdot{}g\in\IC[z] $ $ f\cdot{}g\in\IC[z] $](/teximg/8/0/00388908.png) , wobei , wobei 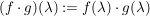 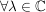 .
(ii) .
(ii) ![$ (\IC[z],+,\cdot{}) $ $ (\IC[z],+,\cdot{}) $](/teximg/3/0/00388903.png) ist ein kommutativer Ring mit Einslement ist ein kommutativer Ring mit Einslement 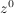 ---
Übg Es sei
---
Übg Es sei 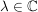  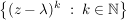 ist ist 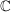 -Vektorraumbasis von -Vektorraumbasis von ![$ \IC[z] $ $ \IC[z] $](/teximg/2/0/00388902.png) ---
---
![$ f\in\IC[z] $ $ f\in\IC[z] $](/teximg/3/1/00388913.png) Def
Def 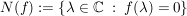 heißt Nullstellenmenge von f. heißt Nullstellenmenge von f.
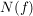 wird auch Menge der Wurzeln (Lösungen) der algebraischen Gleichung f=0 genannt.
---
Übg wird auch Menge der Wurzeln (Lösungen) der algebraischen Gleichung f=0 genannt.
---
Übg 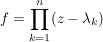 mit mit 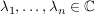  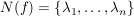 ---
Übg
---
Übg 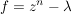 , , 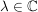 , , 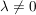
 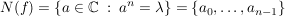 (s.o.) (Folg S1)
Frage: Ist (s.o.) (Folg S1)
Frage: Ist 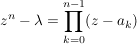 ?
---
__Satz 2 Es sei ?
---
__Satz 2 Es sei ![$ f\in\IC[z] $ $ f\in\IC[z] $](/teximg/3/1/00388913.png) , ,  , , 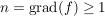
Dann gilt: Es gibt 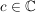 , , 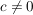 , und , und 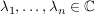 mit mit 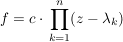
Weiter gilt:
(i) 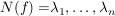
(ii) c ist eindeutig bestimmt und 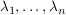 sind eindeutig bis auf die Reihenfolge sind eindeutig bis auf die Reihenfolge
Minimumprinzip
Ist 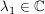 mit mit 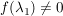 so gilt: so gilt:
Zu  existiert existiert 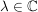 mit mit 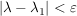 und und 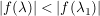
![$ 0\not=f\in\IC[z] $ $ 0\not=f\in\IC[z] $](/teximg/7/2/00388927.png) , , 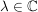 , , 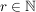
Def 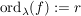 , wenn gilt: , wenn gilt:
![$ f\in(z-\lambda)^r\cdot{}\IC[z] $ $ f\in(z-\lambda)^r\cdot{}\IC[z] $](/teximg/9/2/00388929.png)
![$ f\in(z-\lambda)^{r+1}\cdot{}\IC[z] $ $ f\in(z-\lambda)^{r+1}\cdot{}\IC[z] $](/teximg/0/3/00388930.png)
Man nennt 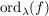 die Nullstellenordnung von f im Punkt die Nullstellenordnung von f im Punkt 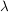 . .
Übg Es sei 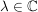 , , 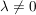 und und 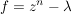
Behauptung: Alle Nullstellen von f sind einfach (d.h. 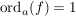 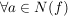 ) )
Es sei ![$ f=\summe_{k=0}^{n} a_k z^k\in\IC[z] $ $ f=\summe_{k=0}^{n} a_k z^k\in\IC[z] $](/teximg/8/2/00388628.png) und und 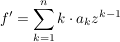
Es sei 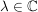 mit mit 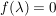
Es gilt: 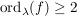  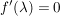
Übg 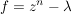 , , 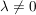 , , 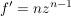
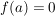  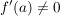  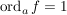
Bem ![$ f\in\IC[z] $ $ f\in\IC[z] $](/teximg/3/1/00388913.png)
Man kann zeigen: 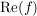 erfüllt auch das Minimumprinzip wobei erfüllt auch das Minimumprinzip wobei  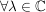
Übg 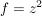 , , 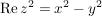 : Graph ist eine Sattelfläche : Graph ist eine Sattelfläche
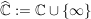 , ( , (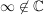 ) )
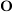 = System der offenen Mengen von = System der offenen Mengen von 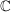
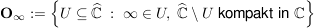
Es gilt: 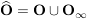 ist das System der offenen Mengen einer Topologie auf ist das System der offenen Mengen einer Topologie auf 
d.h.
(i) 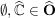
(ii) 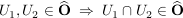
(iii) 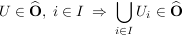
Übg 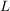 sei eine reelle Gerade in sei eine reelle Gerade in 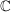
Die abgeschlossene Hülle 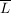 von von 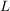 in in 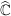 ist ist 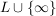
Übg Es sei 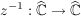 gegeben durch gegeben durch
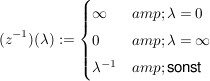
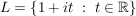
Beh 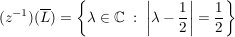
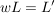
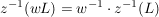
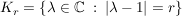 (r>0) (r>0)
Beh 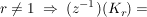 Kreislinie mit Mittelpunkt Kreislinie mit Mittelpunkt 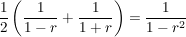
und Radius 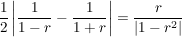
Übg 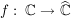 sei stetig, f besitze stetige Fortsetzung sei stetig, f besitze stetige Fortsetzung 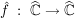
 Ist Ist 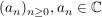 mit mit 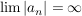 , so gilt: , so gilt: 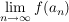 existiert in existiert in 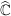 ( (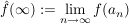 ) )
Übg 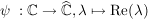 hat keine stetige Fortsetzung auf hat keine stetige Fortsetzung auf 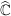 . .
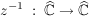
Satz 3: 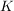 sei Kreislinie in sei Kreislinie in 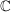 , , 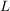 sei Gerade in sei Gerade in 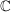 , , 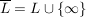
Dann gilt:
(i) Ist 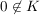 , so ist , so ist 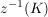 eine Kreislinie eine Kreislinie
(ii) Ist 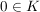 , so ist , so ist 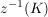 eine Gerade eine Gerade 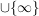
(iii) Ist 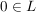 , so ist , so ist 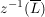 eine Gerade eine Gerade 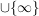
(iv) Ist 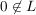 , so ist , so ist 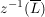 eine Kreislinie in eine Kreislinie in 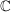 durch 0. durch 0.
Übg
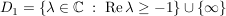
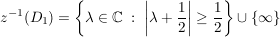
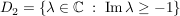
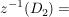 TODO ??? TODO ???
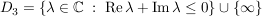
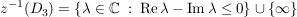
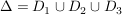 Dreieck mit Ecken -1-i, -1+i, 1-i Dreieck mit Ecken -1-i, -1+i, 1-i
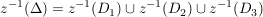
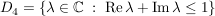
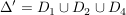
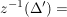
Es sei 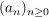 eine Folge in eine Folge in 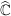 , , 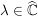
Def 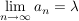 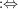 Ist U Umgebung von Ist U Umgebung von 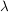 (d.h. existiert offene Teilmenge V von (d.h. existiert offene Teilmenge V von 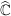 mit mit 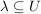 ), so existiert ), so existiert 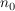 mit: mit:
Übg 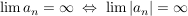 (d.h. (d.h. 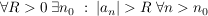 ) )
Übg 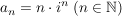
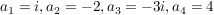
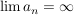
Es gilt: 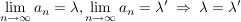
Es sei 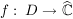 , D offene Teilmenge von , D offene Teilmenge von 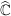 . .
Def f ist stetig, wenn gilt:
Ist U offen in 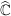 , so ist , so ist 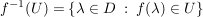 offen in offen in 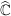 . .
Es gilt: f ist stetig  Ist Ist 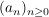 Folge, Folge, 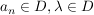 und ist und ist 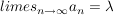 , so ist , so ist 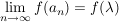
Übg 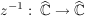 ist stetig ist stetig
Übg 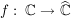 stetig stetig
Es existiert eine stetige Fortsetzung 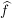 von von  zu Abbildung zu Abbildung 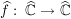 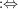 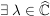 mit: Ist mit: Ist 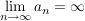 , so ist , so ist 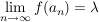
Übg 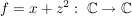
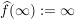
 für für 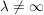
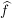 ist stetig ist stetig
Übg 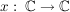 nicht stetig fortsetzbar nicht stetig fortsetzbar
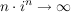 , aber , aber 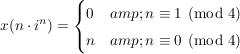
Satz 4 Es seien ![$ f,g\in\IC[z], g\not=0 $ $ f,g\in\IC[z], g\not=0 $](/teximg/7/1/00389017.png) , und , und 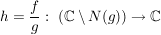 gegeben durch gegeben durch 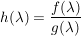 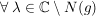
Dann gilt: Es gibt genau eine stetige Abbildung 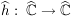 mit mit 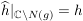
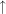 Inhaltsverzeichnis Inhaltsverzeichnis  §2 Komplex differenzierbare Funktionen §2 Komplex differenzierbare Funktionen
|